|
(PDF)
For purposes of applications in calculus and physics, a vector has both a direction and a magnitude (length) and is usually represented by an arrow. The start of the arrow is the vector's foot, and the end is its head. A vector is usually labelled in boldface, such as v.
In an xy-axis system (R2), a vector is written v = 〈v1, v2〉, which means that from the foot of v, move v1 units in the x direction, and v2 units in the y direction, to arrive at the vector's head. The values v1 and v2 are the vector's components. In R3, a vector has three components and is written v = 〈v1, v2, v3〉.
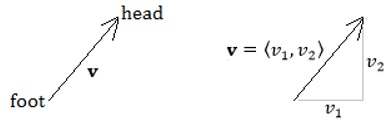
Given two points, P0 = (x0, y0) and P1 = (x1, y1) in R2, a vector P0P1 can be drawn with its foot at P0 and head at P1, where P0 P1 = 〈x1 − x0, y1 − y0〉. In R3, the vector is expressed P0P1 = 〈x1 − x0, y1 − y0, z1 − z0〉. 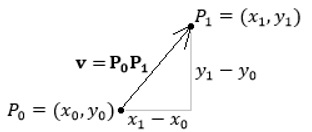
By comparison, a scalar is a number only, with no implied direction. Scalars are chosen from the set of real numbers R. The magnitude of a vector v is found by the Pythagorean Formula: 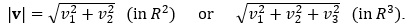
The notation |v| represents the magnitude of v and is always a non-negative value. The expression |v| is a scalar. To add two vectors u = 〈u1, u2, u3〉 and v = 〈v1, v2, v3〉, add the respective components: Place the foot of v at the head of u, then sketch a vector that begins at the foot of u and ends at the head of v. The vector u + v is called the resultant. 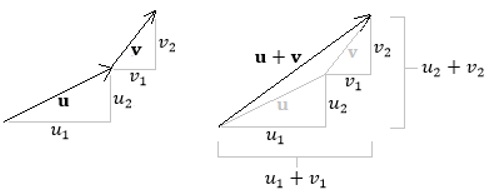
Pay attention to notation. Parentheses ( ) are used to represent points, and angled brackets 〈 〉 are used to represent vectors. A vector may be multiplied by any real number c, called a scalar multiple. For example, if u is a vector, then 2u = u + u = 〈2u1, 2u2〉, which results in a vector 2u that is twice the magnitude of u. Scalars act as coefficients when multiplied to a vector. In general, for a vector v and a scalar c, the magnitude of cv is |cv| = |c||v|, where |c| is the absolute value of c. Two non-zero vectors u and v are parallel if one can be written as a scalar multiple of the other, u = cv for some non-zero scalar c. There are two closure properties of vectors: • C1. Closure across Sums: If u and v are two vectors in R2 (or R3), then their vector sum u + v is also in R2 (or R3). • C2. Closure across Scalar Multiples: If u is a vector in R2 (or R3), then for any scalar c, its scalar multiple cu is also in R2 (or R3). The structural properties of vectors are: • P1. Commutativity: u + v = v + u. Vectors can be added in any order. • P2. Associativity: (u + v) + w = u + (v + w). • P3. Additive Identity: 0 = 〈0,0〉 or 〈0,0,0〉, with the property that u + 0 = 0 + u = u. Thus, 0 is called the zero vector, and is a single point, with a magnitude of 0: |0| = 0, and if |v| = 0, then v = 0. • P4. Additive Inverse: For any non-zero vector u, the vector − u exists with the property that u + ( − u) = 0. Visually, − u has the same magnitude as u, but points in the opposite direction. Subtraction of two vectors is now defined: u − v = u + ( − v) = u + ( − 1v). • P5. Distributivity of a scalar across vectors: If c is a scalar, then c(u + v) = cu + cv. • P6. Distributivity of a vector across scalars: If c and d are scalars, then (c + d)u = cu + du. • P7. Associativity and Commutativity of Scalars: cdu = c(du) = (cd)u = d(cu) = dcu. • P8. Multiplicative scalar identity: 1v = v. Any set V for which the two closure properties and the eight structural properties are true for all elements in V and for all real-number scalars is called a vector space. Elements of a vector space are called vectors. Common vector spaces are Rn, where n is any non-negative integer. Thus, the xy-axis system R2 is a vector space, where any ordered pair (a, b) can be thought of as a vector from (0,0) to (a, b). In this manner, the elements of R2 are vectors of the form 〈a, b〉, and all of the closure and structural properties listed above are met. Similarly, for R3, the real line R1 (= R), and even the trivial space R0 = 0 are vector spaces. Given any non-zero vector v, the unit vector of v is found by multiplying v by 1/|v|. The unit vector has magnitude 1. That is, |v/|v|| = (1/|v|)|v| = 1. The unit vector of v is any vector of length 1 parallel and in the same direction to v. Common notation for the unit vector of v is vunit. In R2, the vectors i = 〈1,0〉 and j = 〈0,1〉 are called the standard orthonormal basis vectors, which allows us to write a vector v = 〈v1, v2〉 = v1i + v2j. In R3, the standard orthonormal basis vectors are i = 〈1,0,0〉, j = 〈0,1,0〉 and k = 〈0,0,1〉. The notation 〈v1, v2〉 and v1i + v2j to represent a vector in R2 can be used interchangeably. Example 6.1: Sketch u = 〈2,3〉 = 2i + 3j. Solution: From any starting point, move 2 units in the x (horizontal) direction, and 3 units in the y (vertical) direction. Below are five copies of the vector u. 
The foot can be placed anywhere. Multiple copies of the same vector can be drawn using different starting points. The position of a vector relative to a coordinate axis system is not relevant. As long as its direction and magnitude are not changed, it is considered to be the same vector. Example 6.2: Given v = 〈4, − 5〉, find |v|, and the unit vector of v. Solution: The magnitude of v is |v| = √((4)2 + ( − 5)2 ) = √(16 + 25) = √41. The unit vector of v is vunit = (1/√(41))〈4, − 5〉 = 〈4/√(41), − 5/√(41)〉. Example 6.3: Find a vector whose foot is A = ( − 1,4) and head is B = (5,2). Solution: The vector is AB = 〈5 − (−1),2 − 4〉 = 〈6,−2〉. Note that BA = −AB, has its foot at B, head at A, and is BA = −〈6,−2〉 = 〈−6,2〉. Vectors AB and BA are parallel, but not in the same direction. 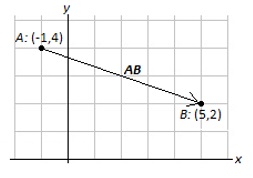
Example 6.4: Given u = 〈−2,1〉 and v = 〈1,5〉, Find and sketch (a) u + v, and (b) u − v. Solution: We have u + v = 〈−2 + 1, 1 + 5〉 = 〈−1,6〉 and u − v = 〈−2 − 1, 1 − 5〉 = 〈−3,−4〉. 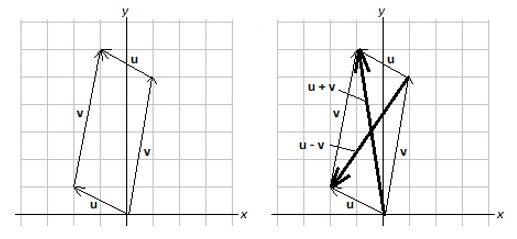
Vectors u and v form a parallelogram, with u + v as one diagonal inside the parallelogram, and u − v the other diagonal. If u and v have a common foot, then u − v has its foot at the head of v, and its head at the head of u. Example 6.5: Given v = 〈3,1〉, Find and sketch (a) 2v and (b) −3v. Solution: We have 2v = 〈2(3),2(1)〉 = 〈6,2〉 and −3v = 〈−3(3),−3(1)〉 = 〈−9,−3〉. 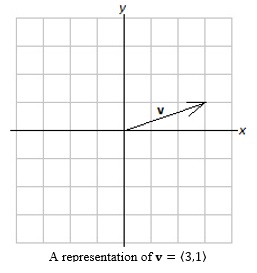
Note that 2v has twice the magnitude of v, and −3v has three times the magnitude of v, pointing in the opposite direction. Vectors 2v, −3v and v are all parallel. Example 6.6: Given u = 〈1,−4,2〉 and v = 〈−5,8,3〉, find 4u − 3v. Solution: We have
Example 6.7: Given the vectors u = 〈1,−4,2〉 and v = 〈−5,8,3〉, find w where 3w + 2u = −v. Solution: Using algebraic manipulation, solve for w: 3w = −v − 2u w = (−1/3)v − (2/3)u. Now, substitute u and v, and simplify:
Example 6.8: Given v = 〈1,2,4〉, find a unit vector in the opposite direction of v. Solution: The magnitude is |v| = √(12 + 22 + 42) = √21. A leading negative sign will cause the vector to point in the opposite direction. Thus,
Example 6.9: Find a vector in the opposite direction of u = 〈−2,1〉 that is 4 times the length of u. Solution: Multiply by −4, where the 4 increases the magnitude by a factor of 4, and the negative reverses the direction: −4u = −4〈−2,1〉 = 〈8,−4〉. Example 6.10: Given v = 〈−1,5,2〉, find a vector w in the same direction as v, with magnitude 3. Solution: The unit vector is vunit = (1/√30)〈−1,5,2〉. Then multiply by 3: In many situations, it is easier to leave any scalar multipliers at the front of the vector, rather than distributing it among the components. Example 6.11: A boat travels north at 30 miles per hour. Meanwhile, the current is moving toward the east at 5 miles per hour. If the boat's captain does not account for the current, the boat will drift to the east of its intended destination. After two hours, find (a) the boat's position as a vector, (b) the distance the boat travelled, and (c) the boat's position as a bearing. Solution: Superimpose an xy-axis system, so that the positive y-axis is North, and the positive x-axis is East. Thus, the boat's vector can be represented by b = 〈0,30〉, and the current's vector by c = 〈5,0〉. a) The boat's position after two hours will be 2(b + c) = 2〈5,30〉 = 〈10,60〉. From the boat's starting point, the boat moved 10 miles east and 60 miles north. b) The boat travelled a distance of |2(b + c)| = 2√(52 + 302) = 2√925, or about 60.83 miles. c) Viewing a drawing below, we see that we can find the angle t using inverse trigonometry. Thus, t = arctan (10/60) = 9.46 degrees East of North. 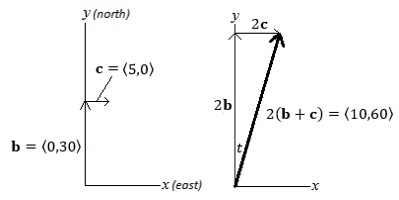
Example 6.12: A 10 kg mass hangs by two symmetric cables from a ceiling such that the cables meet at a 40-degree angle at the mass itself. Find the tension (in Newtons) on each cable. 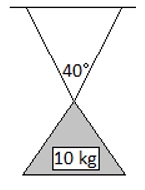
Solution: The force of the mass with respect to gravity is F= ma = (10 kg)(9.8 m/s2) = 98 N. Let |T| be the tension on one cable. We decompose |T| into its vertical and horizontal components: 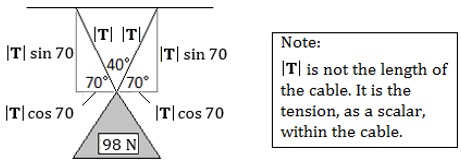
The two horizontal components sum to 0, since the forces cancel one another, while the two vertical components support the 98 N downward force. Thus, we have Solving for |T| we, we obtain Each cable has a tension of about 52.14 N. If the angle at which the cables meet was larger, the tensions would be greater. For example, if the cables were to meet at the mass at an angle of 150 degrees, then each cable would have a tension of
Example 6.13: A mass with a downward force of 100 N is being supported by two cables at full tension as shown in the diagram below. Let |T| represent the tension in one cable, and |U| the tension in the other cable. Find |T| and |U|. 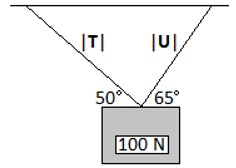
Solution: Decompose |T| and |U|: 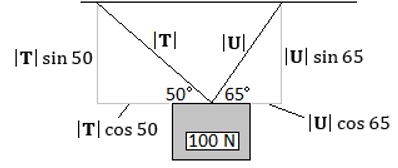
In doing so, we obtain two equations. The horizontal forces sum to 0, and since one force acts in the opposite direction of the other, we have |T| cos 50° − |U| cos 65° = 0. At the same time, the two vertical forces support the 100 N force, so we have |T| sin 50° + |U| sin 65° = 100. This is a system of two equations and two unknowns, |T| and |U|: |T| sin 50° + |U| sin 65° = 100. Multiplying the top by sin 65° and the bottom by cos 65°, we have |T| sin 50° cos 65° + |U| sin 65° cos 65° = 100 cos 65°. Summing the two equations, we have Now we can isolate |T|: To find |U|, we use the first equation of the system, |T| cos 50° − |U| cos 65° = 0, solve for |U|, and substitute |T| = 46.63 N. We have
Example 6.14: An object with a weight of 75 lbs hangs at the center of a cable that is supported at opposite ends by poles 30 feet apart such that the cable meets the poles at the same height. Assume the weight sits in the center and causes a sag of 2 feet. Find the tension in each half of the cable. Solution: A diagram helps us see the situation. 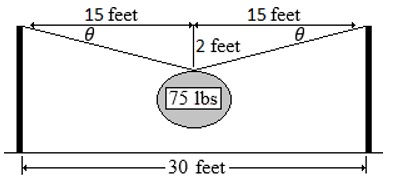
Since this is a symmetric system, the horizontal components of tension sum to 0, while the two vertical components support the 75 lb weight: We are not given the angle θ, but we do know that sin θ = 2/√(22 + 152) = 2/√(229), where √(229) is the length of the hypotenuse of the right triangle, the hypotenuse being the cable under tension. Thus, we have Each cable is supporting 284.78 lbs, which is plausible when considering the large angle at which the two halves of the cable meet at the object. 7. The Dot Product
Let u = 〈u1, u2, u3〉 and v = 〈v1, v2, v3〉 be two vectors. The dot product of u and v, written u · v, is defined in two ways:
• u · v = |u||v| cos θ, where θ is the angle formed when the feet of u and v are placed together;
• u · v = u1v1 + u2v2 + u3v3.
The two forms are equivalent and related to one another by the Law of Cosines. We often don't know the angle between the two vectors, so we tend to use the second formula. However, we may use the first formula to find the angle between vectors u and v. Note that the dot product u · v results in a scalar value.
Some common properties of the dot product are:
• Commutativity: u · v = v · u.
• Distributive property: u · (v + w) = u · v + u · w.
• Scalars can be combined by multiplication: cu · dv = cd(u · v).
• Relation to magnitude: u · u = |u|2.
The most useful feature of the dot product is its sign:
• If u · v > 0, then the angle θ between vectors u and v is acute (0 < θ < π/2).
• If u · v < 0, then the angle θ between vectors u and v is obtuse (π/2 < θ < π).
• If u · v = 0 (assuming u and v are non-zero vectors), then the angle θ between vectors u and v is right (θ = π/2), and the two vectors are orthogonal to one another.
Be aware of notation. The dot product is defined between two vectors and is always written with the dot (·) symbol. Traditional scalar multiplication is written without the dot symbol. Thus, statements like u · v and cu are well defined, while statements like uv and c · u are not defined. Example 7.1: Let u = 〈1,−2,−5〉 and v = 〈3,4,−2〉. Find (a) u · v, and (b) the angle θ between u and v. Solution: a) We use the second definition of the dot product: Since the dot product is positive, we know that the angle between u and v is acute. b) We use the first definition of the dot product, solving for θ: Example 7.2: Suppose 12 vectors of equal magnitude are arranged on an analog clock, such that all vectors have a common foot at the center. The vectors point to 12 o'clock, 1 o'clock, and so on. a) Would the dot product of the vectors pointing to 2 o'clock and 4 o'clock be positive, negative, or zero? Why? b) Would the dot product of the vectors pointing to 10 o'clock and 1 o'clock be positive, negative, or zero? Why? c) Would the dot product of the vectors pointing to 5 o'clock and 9 o'clock be positive, negative, or zero? Why? Solution: a) The two vectors form an acute angle, so their dot product is positive. b) The two vectors form a right angle, so their dot product is zero. c) The two vectors form an obtuse angle, so their dot product is negative. Example 7.3: Let u = 〈8,2,3〉 and v = 〈−3,k,6〉. Find k so that u and v are orthogonal. Solution: Since u and v are orthogonal, their dot product is 0: (8)(−3) + (2)(k) + (3)(6) = 0 −24 + 2k + 18 = 0 2k − 6 = 0 k = 3. Thus, the vectors u = 〈8,2,3〉 and v = 〈−3,3,6〉 are orthogonal. Example 7.4: Suppose vector u has magnitude 6. What is u · u? Solution: Use the relationship u · u = |u|2. Since |u| = 6, then u · u = 62 = 36. Example 7.5: Let u = 〈−1,4,6〉 and v = 〈3,2,−4〉. Find all possible vectors w that are orthogonal to both u and v. Solution: Let w = 〈x, y, z〉. Since w is orthogonal to u, and orthogonal to v, we know that u · w = 0 and v · w = 0. 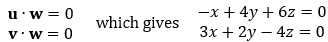
This is a system of two equations in three variables. Let x = t (a constant). Now we have a system of two equations in two variables. Here, we eliminate the y variable first: 
Thus, z = (1/2)t. Using the equation 4y + 6z = t where z = (1/2)t, we obtain 4y + 6((1/2)t) = t, which, after algebra, gives y = (−1/2)t. We now have vector w identified: 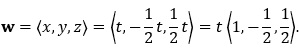
There are infinitely many vectors w that are simultaneously orthogonal to u = 〈−1,4,6〉 and v = 〈3,10,−2〉, and they are all scalar multiples of the vector 〈1,−1/2,1/2〉, or 〈2,−1,1〉 if we prefer a vector with integer components. To verify, we show that the dot product of 〈2,−1,1〉 (or any non-zero scalar multiple thereof) with u and with v is 0: and that
Example 7.6: Let u = 〈1,−4,2〉. Find all possible vectors v orthogonal to u. Solution: Let v = 〈x, y, z〉. Since u and v are orthogonal, we have u · v = 0: Let y = s and z = t. This is a system where x, y and z are written in terms of s and t: y = s z = t. Now, zero-fill so that columns are evident: 
Thus, any vector v that is orthogonal to u = 〈1,−4,2〉 is of the form Here, s and t are parameter variables, chosen independently of one another. For example, if we arbitrarily let s = −4 and t = 9, we have It is easy to verify that v = 〈−34,−4,9〉 is orthogonal to u = 〈1,−4,2〉: Thus, we now have a "formula" that can generate all possible vectors v that are orthogonal to u = 〈1,−4,2〉. Try it with any other choices of s and t.
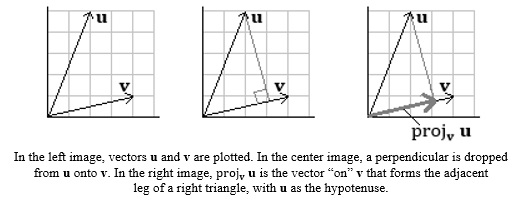
8. Projections Given two vectors u and v, the orthogonal projection (or projection) of u onto v is given by Think of a right triangle: u is the hypotenuse, and projv u is the adjacent leg of the triangle that points in the direction of v. The opposite leg, called normv u, is found by vector summation: 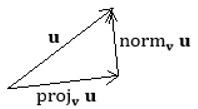
Since projv u + normv u = u, then normv u = u − projv u. Often, we need to write a vector u in terms of a vector parallel to v, and another vector orthogonal (or normal) to v. This is called decomposition of a vector, and is done using projections. Take care to perform the projection operations in the correct order. When we say "project u onto v", it is vector v that is being altered. Example 8.1: Find the projection of u = 〈2,5〉 onto v = 〈4,1〉. Solution: The projection of u onto v is 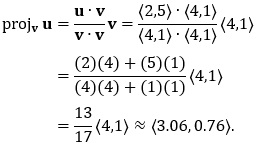
Example 8.2: Decompose u = 〈2,5〉 into two vectors, one parallel to v = 〈4,1〉, and another normal to v = 〈4,1〉. Solution: The vector parallel to v is found by projecting u = 〈2,5〉 onto v = 〈4,1〉. From the previous example, we have projv u = (13/17)〈4,1〉. The vector normal to v is found by vector subtraction: 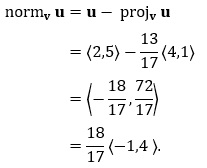
Viewing this as a right triangle, projv u = 13/17 〈4,1〉 and normv u = 18/17 〈−1,4 〉 are the two legs of a right triangle, with u = 〈2,5〉 being the hypotenuse. Example 8.3: Jimmy is standing at the point A = (1,2) and wants to visit his friend who lives at the point B = (7,3), all units in miles. Jimmy starts walking in the direction given by v = 〈4,1〉. If he continues to walk in this direction, he will miss point B. Suppose Jimmy is allowed one right-angle turn. At what point should Jimmy make this right angle turn so that he arrives at point B? Solution: We sketch a diagram to get a sense of Jimmy's location and direction of travel, as well as to see where his right-angle turn should be made. 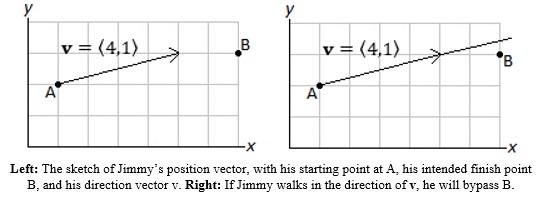
This vector, (25/17)〈4,1〉 = 〈100/17, 25/17〉, can be placed so its foot is at A = (1,2). Thus, its head will be at (1 + 100/17, 2 + 25/17) = (117/17, 59/17), or about (6.88, 3.47), which agrees well with the diagram. This is where Jimmy should make his right-angle turn. 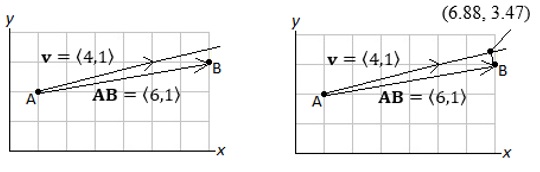
Jimmy will walk a distance of |projv AB| = |〈100/17, 25/17〉| = √((100/17)2 + (25/17)2), or about 6.06 miles in the direction of v, and then walk |normv AB| = √((7 − 117/17)2 + (3 − 59/17)2 ), about 0.49 miles orthogonal to v. 9. The Cross Product Let u = 〈u1, u2, u3 〉 and v = 〈v1, v2, v3 〉 be two vectors in R3. The cross product of u and v is denoted u × v and is defined by the formula The cross product is a vector that is simultaneously orthogonal to u and to v. Since it is easy to make a calculation error when finding the cross product, check your work by showing the result is orthogonal with the two original vectors. The calculation of the cross product is best memorized as the determinant of a 3 by 3 matrix: 
Don't forget the negative in front of the j term. The cross product vector, u × v, points in a direction as defined by the "right hand rule". Curling one's fingers on their right hand from u to v, the cross product vector will point in the direction of the thumb pointing away from the palm. Some of the common properties of the cross product are: • Switching the order of the vectors results in a factor of −1 u × v = −(v × u). The cross product is not commutative. • Scalars can be grouped to the front: cu × dv = cd(u × v). • Distributive property: u × (v + w) = u × v + u × w. • The magnitude of the cross product is |u × v | = |u||v| sin θ. It is the area of the parallelogram formed by u and v. A corollary to the last property is that if u and v are parallel, then u × v = 0. If vectors u and v are in R2, then the cross product is defined if the vectors are rewritten as u = 〈u1, u2, 0〉 and v = 〈v1, v2, 0〉. In this case, the result is u × v = 〈0, 0, u1v2 − u2v1〉. Example 9.1: In the image below, vectors u, v and w are drawn. State whether the cross products (a) u × v, (b) u × w and (c) w × v are positive (coming out of the paper), negative (going into the paper) or 0. 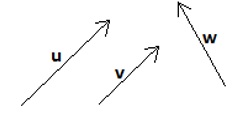
Solution: (a) Since u and v are parallel, u × v = 0; (b) Placing the feet of u and w together, curl your fingers from u to w. Your thumb will point upwards, out of the paper, so u × w is positive. (c) placing the feet of w and v together, you have to invert your hand in order to curl your fingers from w towards v. Thus, your thumb would point down, or into the paper, and w × v is negative. Example 9.2: Let u = 〈−1,4,6〉 and v = 〈3,2,−4〉. Find u × v . Solution: We have 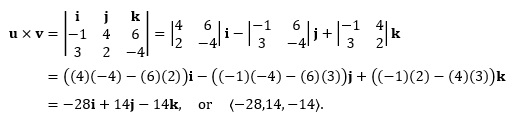
Check that this is correct by showing (u × v) · u = 0 and (u × v) · v = 0: 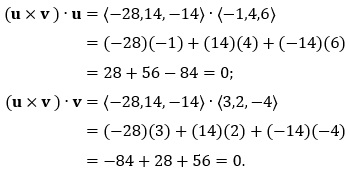
Thus, u × v = 〈−28,14,−14〉 is orthogonal to u and orthogonal to v. In Example 7.5, we showed that there are infinitely many vectors that are orthogonal to u = 〈−1,4,6〉 and v = 〈3,2,−4〉, all having the form t〈1,−1/2,1/2〉. Note that 〈−28,14,−14〉 is one such vector, when t = −28. Example 9.3: Let u = 〈−1,4,6〉 and v = 〈3,2,−4〉. Find the area of the parallelogram formed by u and v, then find the area of the triangle formed by u and v. Solution: From the previous example, we have u × v = 〈−28,14,−14〉. Thus, the area of the parallelogram formed by u and v is 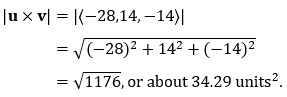
The area of the triangle formed by u and v is half this quantity, (1/2)√(1176), or about 17.145 square units. Example 9.4: Find the area of the triangle formed by the points A = (1,3,−2), B = (4,0,3) and C = (6,−3,5). Solution: We form two vectors from among the three points (any pair of vectors will suffice). The vector from A to B is AB = 〈3,−3,5〉, and the vector from A to C is AC = 〈5,−6,7〉. The cross product of AB and AC is 
(Check that this is correct by verifying that (AB × AC) · AB = 0 and (AB × AC) · AC = 0.) The area of the triangle is half the magnitude of AB × AC: Other vectors formed from points A, B and C will work. For example, try this with vectors BA and CB. 10. The Scalar Triple Product Let u = 〈u1, u2, u3〉, v = 〈v1, v2, v3〉 and w = 〈w1, w2, w3〉 be three vectors in R3. The scalar triple product of u, v and w is given by 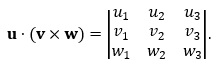
The scalar triple product is a scalar quantity. Its absolute value is the volume of the parallelepiped (a "tilted" box) formed by u, v and w. The ordering of the vectors is not important. For example, result in values that differ by at most the factor −1. Example 10.1: Find the volume of the parallelepiped with sides represented by the vectors u = 〈−1,3,2〉, v = 〈4,2,−5〉 and w = 〈0,−3,1〉. Solution: We have 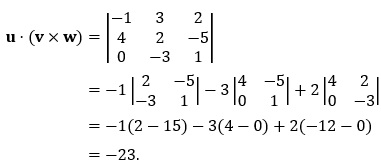
Taking the absolute value, the volume is 23 cubic units. Example 10.2: Four ordered triples, A = (3,2,1), B = (−2,5,4), C = (6,10,1) and D = (0,7,−4) form a tetrahedron, a four-sided solid in which each face is a triangle. Find the volume of this tetrahedron. Solution: The volume of a tetrahedron is one-sixth the volume of a parallelepiped. We find three vectors, and then find their scalar triple product. Next, we have: 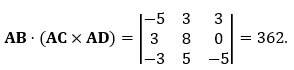
Thus, the volume of the tetrahedron is (1/6)(362) = 181/3 = 60 & 1/3 cubic units. Example 10.3: Find the volume of the parallelepiped with sides represented by the vectors u = 〈2,1,3〉, v = 〈−5,2,1〉 and w = 〈−3,3,4〉. Interpret the result. Solution: We have 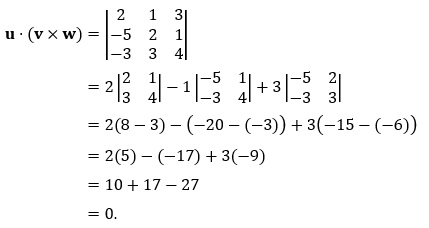
The volume of the parallelepiped formed by u, v and w is 0. The object has no thickness, which would imply that the three vectors are coplanar (lying on a common plane). 11. Work & Torque Work is defined as force F (in Newtons) applied to move an object a distance of d (in meters). It is the product of F and d: The standard metric unit for work is Joules, which is equivalent to Newton-meters. If the force is not applied in the same direction that the object will move, then we need to find the component of F (written now as a vector) that is parallel to the direction d, also now written as a vector. Placing the feet of F and d together, the component of F in the direction of d is given by |F| cos θ. If |d| is the length of vector d (not necessarily the distance moved by the object in the direction of d), then the work is given by This is the dot product of F and d. Thus, work can be defined as a dot product, Work is a scalar value. It may be a negative value, which can be interpreted that the object is moving against the force being applied to it. For example, walking into a headwind at an angle. Example 11.1: A force of 10 Newtons is applied in the direction of 〈1,1〉 to an object that moves in the direction of the positive x-axis for 5 meters. Find the work performed on this object. Solution: Using geometry, the component of the force in the direction of the positive x-axis is |F| cos (π/4) = 10(√(2)/2) = 5√(2). The object moves 5 meters, so the work performed is Using vectors, the force vector is F = 〈10/√2, 10/√2〉 and the direction vector is d = 〈5,0〉. Thus, the work performed is Example 11.2: A force of 50 N is applied in the direction of the positive x-axis, moving an object 10 meters up an inclined plane of 30 degrees. Find the work. Solution: Using geometry, the component of the force that is parallel to the inclined ramp is 50 cos 30° = 50(√(3)/2) = 25√(3) N. This component of the force moves the object 10 m, so the total work performed is Using vectors, the force is given by F = 〈50,0〉 while the 10-meter ramp inclined at 30 degrees has is described by the vector d = 〈10 cos 30°, 10 sin 30°〉. Thus the work performed is Torque describes the force resulting from a pivoting motion. For example, when a wrench is turned around a pivot point (e.g. a bolt), it creates a force in the direction of the bolt. If the wrench is described as a vector r (where the length of the wrench is |r|) and the force applied to the wrench as another vector F (with magnitude |F|), then the torque τ (tau) is orthogonal to both r and F, defined by the cross product: This means that torque τ is a vector. However, if bothrand F lie in the xy-plane, then τ is a vector of the form 〈0,0,k〉, and its magnitude is |τ| = k. This scalar value is usually given as the torque in place of its vector form. It makes intuitive sense that the force F applied to a wrench r (or anything that turns on a pivot) should be orthogonal to r. If F is not orthogonal to r, then we look for the component of F that is orthogonal to r. This component of F is what "turns the wrench", so to speak. In the following images, vectors r and F are both drawn with their feet at a common point, the pivot point. The angle between r and F is θ. Naturally, we would not apply the force F at the pivot itself. Recall that a vector can be moved at will, so we locate F so that its foot is at r's head. Now we look for the component of the magnitude of F that is orthogonal to r. We see that it is |F| sin θ. If |r| is the length of the wrench, then the area given by |F||r|sin θ is interpreted as the torque, as a scalar. This is |τ| = |r × F|. 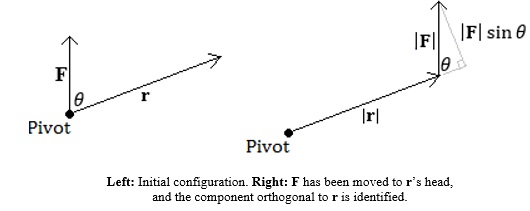
Also note that in this example, r × F points out of the page. This force F will turnrin a counter-clockwise direction, and in the usual sense of a wrench turning a bolt, this will loosen the bolt — i.e. it will emerge from this page. Since F is in Newtons, thenrmust be in meters to maintain consistency in units. The units for torque are Newton-meters, abbreviated Nm. Example 11.3: Find the torque around the pivot shown in the following diagram. 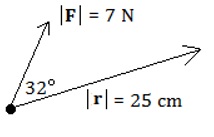
Solution: We convert the magnitude of r into meters. Thus, the torque is Example 11.4: Find the torque around the pivot shown in the following diagram. 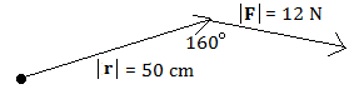
Solution: Note the position of the force vector F relative to r. Although it is reasonable to assume that to turn r around its pivot, we would apply the force F at its head, the angle given in the diagram must be handled carefully. The desired angle θ is defined by placing the feet of F and r at a common point. In other words, the equation |τ| = |F||r| sin θ = (12)(0.5) sin (160°) is incorrect. Instead, redraw the diagram slightly, placing the foot of F at the pivot: 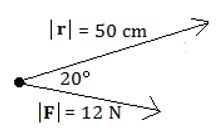
The desired angle is 20°. Thus, the torque is |τ| = |F||r| sin θ = (12)(0.5) sin (20°) = 2.05 Nm.
|