|
(PDF)
On Earth, the gravitational acceleration constant is −9.8 meters per second per second (or m⁄s2). If we superimpose an xy-axis system with the positive y axis being "up", then acceleration can be written as a vector-valued function, The x-component of acceleration is 0, since falling bodies will not accelerate horizontally due to gravity. Note that both components are constants. Integrating acceleration, we get velocity, which is also a vector-valued function: Here, 〈vx ,vy 〉 are constants of integration and represents the initial velocity in the x-direction and in the y-direction, respectively. Speed is the magnitude of velocity. Speed is a scalar value. Integrating velocity, we get displacement (or position), also a vector-valued function: Similar to above, 〈rx,ry〉 represent the initial position of the object in the x-direction and y-direction respectively. The placement of the origin is arbitrary but is usually done so that rx = 0 since it is almost always practical to assume no initial horizontal distance. A typical object that is released and then allowed to return to earth under gravity alone will follow a parabolic arc. Its position vector r(t), velocity vector v(t) and acceleration vector a(t) are a "tool kit" of equations that completely describes the motion of the object. In most projectile motion situations, we assume that air friction is ignored, any spin on the object is not considered, and that time t is in seconds and is usually reckoned from t = 0, representing when the object was released. Here are some common questions that may be posed regarding a falling object:
Build the complete set of displacement, velocity and acceleration vectors first, before solving any subsequent questions. Example 22.1: A ball is propelled off a 100 m tall cliff at an initial speed of 50 meters per second at an angle of 30 degrees above the horizontal.
Solution: Starting with acceleration, a(t) = 〈0, −9.8〉, integrate to obtain To find vx and vy , note that its initial speed is |v(0)| = 50 at an angle of 30 degrees. This suggests a right triangle, in which |v(0)| = 50 is the hypotenuse, and vx and vy are the horizontal and vertical legs, respectively. 
Thus, vx = 50 cos (30) = 25√3 = 43.301, and vy = 50 sin (30) = 25, and the velocity vector is Integrating v, we obtain the displacement vector Since the ball was thrown off the top of a cliff, set the origin at the base of the cliff, so that rx = 0 and ry = 100. Therefore, the displacement vector is We now have sufficient information to answer the posed questions. In all cases, assume t ≥ 0. The ball reaches its maximum height when the y-component of velocity is 0 since the ball's vertical velocity is 0 (momentarily stops) when it reaches it maximum height. Thus, we solve −9.8t + 25 = 0 to find when the ball has reached its maximum height. This happens at t = 25/9.8 = 2.551 seconds. Substituting this into the y-component of displacement, we now determine the height of the ball at this time: The ball impacts the ground when the y-component of displacement is 0. We use the quadratic formula to find the roots of −4.9t2 + 25t + 100 = 0: The negative result is ignored. The ball lands at t = 7.739 seconds. The range in which the ball travelled from the base is found by evaluating the x-component of displacement by this t: We find the velocity at t = 7.739 seconds: The impact speed of the ball is the magnitude of this vector: To find the angle at which the ball impacts the ground, sketch a diagram to be sure that the components of velocity are properly in place: 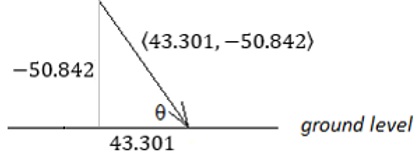
The angle of impact is θ = tan−1((−50.842)/43.301) = −49.6 degrees. The negatives can be ignored, so that the impact angle is 49.6 degrees. Example 22.2: An airplane is flying horizontally 5,000 meters above flat ground at a velocity of 300 kilometers per hour. An object is released below the airplane and allowed to fall to earth.
Solution: We need to convert 300 kilometers per hour into meters per second: The initial velocity is therefore v(0) = 〈vx , vy 〉 = 〈250/3,0〉, where the 0 in the y-component suggests that the object was merely released with no initial push in the vertical direction. Integrating the acceleration vector a(t) = 〈0, −9.8〉, the velocity vector is For initial position, the object was released 5000 meters above the ground suggests that ry = 5000, while rx = 0. Therefore, the displacement function is The object is airborne for the time needed for the y-component of displacement to equal 0 meters, the height of the ground. Thus, we have Solving, we get t = √(5000/4.9) = 31.944 seconds. The range is found by evaluating the x-component of displacement at t = 31.944 seconds. We find that the object travelled (250/3)(31.944) = 2,662 meters. Example 22.3: A cannon is angled at 25 degrees above the flat ground. A cannonball is shot from this cannon, and it lands 50 meters downrange. Assume the cannonball left the cannon 1 meter above the ground.
Solution: Let v0 represent the initial speed. Using trigonometry, the x and y components of the initial velocity are vx =v0 cos (25°) and vy =v0 sin (25°). Therefore, the velocity vector is By placing the origin directly below where the cannonball began its trajectory, we have rx = 0 and ry = 1. The displacement vector is The cannonball landed 50 meters downrange, so the x-component of displacement is set equal to 50, and we can find an expression for t in terms of v0: When the cannonball landed, the y-component of displacement is 0 meters, so we have −4.9t2 + (v0 sin (25°))t + 1 = 0. Now substitute t = 50/(v0 cos (25°)) into this equation, simplify, and solve for v0: (−12,250)/(v02 cos2 (25°)) + (50 sin (25°))/cos (25°) = −1 Multiply by the common denominator, v02 cos2 (25°) to clear fractions: Collect terms: Isolate v0: The cannonball left the cannon at a speed of about 24.766 meters per second. Since t = 50/(v0 cos (25°)) and v0 = 24.766, we have t = 50/((24.766) cos (25°)) = 2.228 seconds. This is the time the cannonball was in the air. The maximum height occurs when the y-component of velocity is 0: t = (24.766 sin (25°))/9.8 = 1.068 seconds. This is substituted into the y-component of displacement: • • • • • • • • • • • Example 22.4: An object is projected from the top of a 50-meter-tall cliff. It remains in the air for 8 seconds, landing 250 meters downrange. Find the following:
Solution: Starting with a(t) = 〈0, −9.8〉, we develop vector-valued functions for v(t) and r(t): where 〈vx ,vy 〉 are the initial components of the velocity when the object is released, and 〈rx,ry 〉 is its initial position. By setting the origin at the base of the cliff directly below the point where the object was released, we have rx = 0 and ry = 50. Thus, we have At t = 8 seconds, the object lands 250 meters downrange, at which time its vertical component of position will be 0. Thus, we examine the components of r(t): −4.9(8)2 + vy (8) + 50 = 0. From the first equation, we have vx = 250/8 = 31.25 meters per second, and from the second equation, we have vy = ((4.9)(64) − 50)/8 = 32.95 meters per second. We can now identify the velocity and position vectors precisely: With the velocity and position vectors now established, we can now address the questions: The object reaches its maximum height when the y-component of velocity is 0, or when −9.8t + 32.95 = 0, giving t = 32.95/9.8 = 3.362 seconds. This is then evaluated into the y-component of position. The object's maximum height is The initial velocity is v(0) = 〈31.25, 32.95〉. Thus, the initial speed of the object is and its initial angle above the horizontal is • • • • • • • • • • • Example 22.5: An object is propelled off a building that is 75 m high, the object propelled at an initial angle of 40° to the horizontal. It reaches a maximum height after 1.75 seconds. How far downrange does the object land, assuming the ground below to be flat? Solution: We start with velocity v(t) = 〈vx , −9.8t + vy 〉 and position r(t) = 〈vx t + rx, −4.9t2 + vy t + ry〉. Assuming a starting position of 〈vx ,vy 〉 = 〈0,75〉, we can further refine the position vector function as r(t) = 〈vx t, −4.9t2 + vy t + 75〉. From the velocity vector, the object reaches its maximum height when its y-component is 0. Thus, we have −9.8(1.75) + vy = 0, which gives vy = 17.15 meters per second. From this, we can reconstruct the initial velocity components. We have a right triangle with an angle of 40° and an opposite leg of 17.15 meters per second. Thus, the adjacent leg is given by This allows us to completely define the position vector, r(t) = 〈20.439t, −4.9t2 + 17.15t + 75〉, t ≥ 0. The object impacts the ground when the y-component of r(t) is 0: Using the quadratic formula, we get two results: The negative result is ignored. The positive result, 6.036 seconds, is the time after release that the object impacts the ground. Its distance from the base of the building is given by the x-component of position: Thus, the object travelled a total of about 123.37 meters in the horizontal direction before impacting the ground.
Example 22.6: A golf ball is hit from the ground by an astronaut on a distant planet. It reaches a maximum height of 50 meters after 4 seconds of flight. What is the gravitational constant on this planet? Solution: We start with a(t) = 〈0,−a〉, then develop v(t) and r(t): Assume that the initial position is 〈rx ,ry 〉 = 〈0,0〉. Thus, position is given by r(t) = 〈vx t, (−a/2)t2 + vy t〉, t ≥ 0. When the ball reaches the maximum height, its vertical component of velocity is 0, while the vertical component of position is 50. This creates a pair of equations: (−a/2)t2 + vy t = 50. When t = 4, we obtain −4a + vy = 0 and (−a/2)(4)2 + 4vy = 50. From the first equation, we have and from the second equation, we have Solving for a, we obtain 8a = 50 a = 50/8 = 6.25. Evidently, objects on this planet fall at a rate of 6.25 meters per second per second.
|