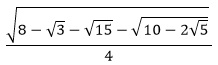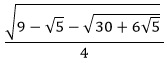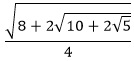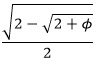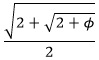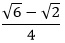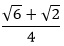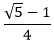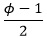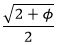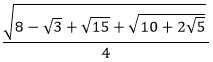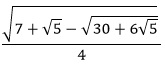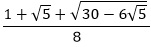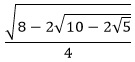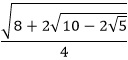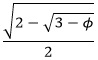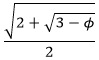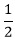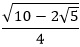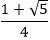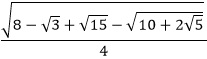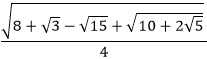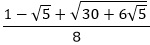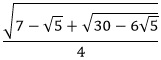|
Exact values of sin x and cos x, where x is in degrees and is a multiple of 3.
The sine and cosine values for all angle measurements in multiples of 3 degrees can be represented in terms of square-root radicals, and the four common operations of arithmetic. These values can be determined geometrically using three strategic triangles.
|
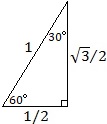
For an equilateral triangle, each of the three interior angles are 60°. Viewing half the triangle gives a 30-60-90 right triangle, with the hypotenuse measuring 1, the short leg 1/2, and the long leg 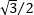 . Using the right-triangle trigonometry definitions sin x = opp/hyp and cos x = adj/hyp, we get sin 30° = 1/2 and cos 30° = . Using the right-triangle trigonometry definitions sin x = opp/hyp and cos x = adj/hyp, we get sin 30° = 1/2 and cos 30° = 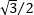 . .
|
|
| |
From a square, with interior angles 90°, draw a diagonal from one corner to its opposite corner. This forms a right triangle with two of the square's sides being the legs of the triangle, and the drawn diagonal being the hypotenuse. Let the hypotenuse be 1 unit in length. Then the legs have length 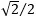 units each. This gives sin 45° = cos 45° = units each. This gives sin 45° = cos 45° = 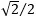 . .
|
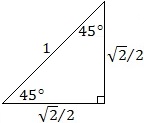
|
| |
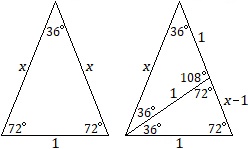
From the isosceles 36-72-72 triangle, let the two long sides be x, and the short side 1. Bisect one of the 72° angles, extending the ray to intersect the other side of the triangle. This forms two triangles: an isosceles 36-36-108 triangle whose short sides are both 1, and a smaller isosceles 36-72-72 triangle whose long sides are 1, and short side is x – 1, as shown in the diagrams at right:
|
|
The two 36-72-72 triangles are proportional: The ratio of the long sides x:1 is the same proportion as the ratio of the short sides: 1:(x – 1). Solve for x by equating two ratios: x/1 = 1/(x – 1), which then gives x2 – x – 1 = 0. Solving for x using the quadratic formula (and ignoring the negative root) gives x =  . Splitting the 36-36-108 triangle in half forms a right triangle, a 36-54-90 triangle, with hypotenuse 1, long leg x/2 and short leg . Splitting the 36-36-108 triangle in half forms a right triangle, a 36-54-90 triangle, with hypotenuse 1, long leg x/2 and short leg 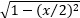 . Since x = . Since x =  , we have: , we have:
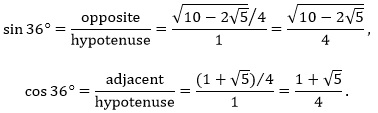
The number  is called the golden ratio and is denoted by the Greek letter φ (lower-case phi). Thus, we can write is called the golden ratio and is denoted by the Greek letter φ (lower-case phi). Thus, we can write
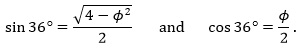
The remaining exact representations for angles of multiples of 3° can now be found, using sum-difference and half-angle identities. Since different identities may be used, the exact representations may "look" different than other possible representations, but can be shown to be identical in value. The following is a sequence of tables of all exact values for the sine and cosine of angles of multiples of 3°, up through 45°. All radicals were simplified so that none contained any quotients within them. Whenever appropriate, the equivalent representation in terms of the golden ratio φ is given.
All of these values are algebraic, meaning they are the root of some polynomial with integer coefficients. For example, sin 90° is algebraic. It equals 1, which is the root of the polynomial x – 1. Given an algebraic number in the form of radicals and arithmetic operations, one can build a polynomial for which the given number is a root. For example, We know that sin 45° = 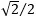 , so we set x = sqrt(2)/2, then square both sides and collect terms to one side, we get x2 – 1/2 = 0. Thus, 2x2 – 1 is a polynomial for which , so we set x = sqrt(2)/2, then square both sides and collect terms to one side, we get x2 – 1/2 = 0. Thus, 2x2 – 1 is a polynomial for which 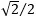 is a root. is a root.
| Angle: 0° or 0 radians |
sin 0° & cos 90° |
cos 0° & sin 90° |
| Value: |
0 |
1 |
| Minimal Polynomial: |
x |
x – 1 |
| Angle: 3° or π/60 radians |
sin 3° & cos 87° |
cos 3° & sin 87° |
| Decimal Approximation: |
0.052335956... |
0.998629534... |
| Exact Representation: |
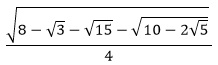 |
 |
| Minimal Polynomial: |
65536x16 – 262144x14 + 430080x12 – 372736x10 + 182784x8 – 50176x6 + 7040x4 – 384x2 + 1
(for both) |
| Angle: 6° or π/30 radians |
sin 6° & cos 84° |
cos 6° & sin 84° |
| Decimal Approximation: |
0.104528463... |
0.994521895... |
| Exact Representation: |
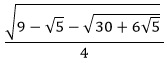 |
 |
| Minimal Polynomial: |
16x4 + 8x3 – 16x2 – 8x + 1 |
256x8 – 448x6 + 224x4 – 32x2 + 1 |
| Angle: 9° or π/20 radians |
sin 9° & cos 81° |
cos 9° & sin 81° |
| Decimal Approximation: |
0.156434465... |
0.987688341... |
| Exact Representation: |
 |
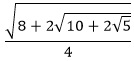 |
| Exact Representation in φ form: |
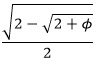 |
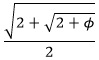 |
| Minimal Polynomial: |
256x8 – 512x6 + 304x4 – 48x2 + 1 |
| Minimal Polynomial in φ form: |
16x4 – 16x2 + 2 – φ |
| Angle: 12° or π/15 radians |
sin 12° & cos 78° |
cos 12° & sin 78° |
| Decimal Approximation: |
0.207911690... |
0.978147600... |
| Exact Representation: |
 |
 |
| Minimal Polynomial: |
256x8 – 448x6 + 224x4 – 32x2 + 1 |
16x4 + 8x3 – 16x2 – 8x + 1 |
| Angle: 15° or π/12 radians |
sin 15° & cos 75° |
cos 15° & sin 75° |
| Decimal Approximation: |
0.258819045... |
0.965925826... |
| Exact Representation: |
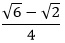 |
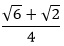 |
| Minimal Polynomial: |
16x4 – 16x2 + 1
(for both) |
| Angle: 18° or π/10 radians |
sin 18° & cos 72° |
cos 18° & sin 72° |
| Decimal Approximation: |
0.309016994... |
0.951056516... |
| Exact Representation: |
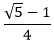 |
 |
| Exact Representation in φ form: |
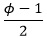 |
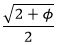 |
| Minimal Polynomial: |
4x2 + 2x – 1 |
16x4 – 20x2 + 5 |
| Angle: 21° or 7π/60 radians |
sin 21° & cos 69° |
cos 21° & sin 69° |
| Decimal Approximation: |
0.358367949... |
0.933580426... |
| Exact Representation: |
 |
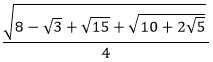 |
| Minimal Polynomial: |
65536x16 – 262144x14 + 430080x12 – 372736x10 + 182784x8 – 50176x6 + 7040x4 – 384x2 + 1
(for both) |
| Angle: 24° or 2π/15 radians |
sin 24° & cos 66° |
cos 24° & sin 66° |
| Decimal Approximation: |
0.406736643... |
0.913545457... |
| Exact Representation: |
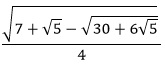 |
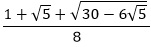 |
| Minimal Polynomial: |
256x8 – 448x6 + 224x4 – 32x2 + 1 |
16x4 – 8x3 – 16x2 + 8x + 1 |
| Angle: 27° or 3π/20 radians |
sin 27° & cos 63° |
cos 27° & sin 63° |
| Decimal Approximation: |
0.453990499... |
0.891006524... |
| Exact Representation: |
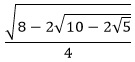 |
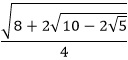 |
| Exact Representation in φ form: |
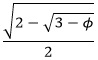 |
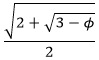 |
| Minimal Polynomial: |
256x8 – 512x6 + 304x4 – 48x2 + 1 |
| Minimal Polynomial in φ form: |
16x4 – 16x2 + 1 + φ |
| Angle: 30° or π/6 radians |
sin 30° & cos 60° |
cos 30° & sin 60° |
| Decimal Approximation: |
0.5 |
0.866025403... |
| Exact Representation: |
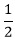 |
 |
| Minimal Polynomial: |
2x – 1 |
4x2 – 3 |
| Angle: 33° or 11π/60 radians |
sin 33° & cos 57° |
cos 33° & sin 57° |
| Decimal Approximation: |
0.544639035... |
0.838670567... |
| Exact Representation: |
 |
 |
| Minimal Polynomial: |
65536x16 – 262144x14 + 430080x12 – 372736x10 + 182784x8 – 50176x6 + 7040x4 – 384x2 + 1
(for both) |
| Angle: 36° or π/5 radians |
sin 36° & cos 54° |
cos 36° & sin 54° |
| Decimal Approximation: |
0.587785252... |
0.809016994... |
| Exact Representation: |
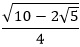 |
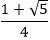 |
| Exact Representation in φ form: |
 |
 |
| Minimal Polynomial: |
16x4 – 20x2 + 5 |
4x2 – 2x – 1 |
| Angle: 39° or 13π/60 radians |
sin 39° & cos 51° |
cos 39° & sin 51° |
| Decimal Approximation: |
0.62932039... |
0.777145961... |
| Exact Representation: |
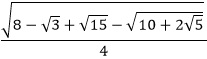 |
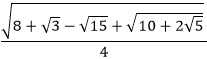 |
| Minimal Polynomial: |
65536x16 – 262144x14 + 430080x12 – 372736x10 + 182784x8 – 50176x6 + 7040x4 – 384x2 + 1
(for both) |
| Angle: 42° or 7π/30 radians |
sin 42° & cos 48° |
cos 42° & sin 48° |
| Decimal Approximation: |
0.669130606... |
0.743144825... |
| Exact Representation: |
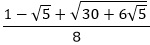 |
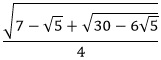 |
| Minimal Polynomial: |
16x4 – 8x3 – 16x2 + 8x + 1 |
256x8 – 448x6 + 224x4 – 32x2 + 1 |
| Angle: 45° or π/4 radians |
sin 45° |
cos 45° |
| Decimal Approximation: |
0.707106781... |
0.707106781... |
| Exact Representation: |
 |
 |
| Minimal Polynomial: |
2x2 – 1 |
2x2 – 1 |
Common Minimal Polynomials
Note that sin 3°, cos 3°, sin 21°, cos 21°, sin 33°, cos 33°, sin 39° and cos 39° all have the same minimal polynomial,
65536x16 – 262144x14 + 430080x12 – 372736x10 + 182784x8 – 50176x6 + 7040x4 – 384x2 + 1.
This polynomial is even (all even powers of x) so that it is symmetric with the y-axis. This means that the polynomial can be factored as
65536(x2 – sin2 3°)(x2 – cos2 3°)(x2 – sin2 21°)(x2 – cos2 21°)(x2 – sin2 33°)(x2 – cos2 33°)(x2 – sin2 39°)(x2 – cos2 39°)
The graph for this function, for 0 < x < 1, is below.
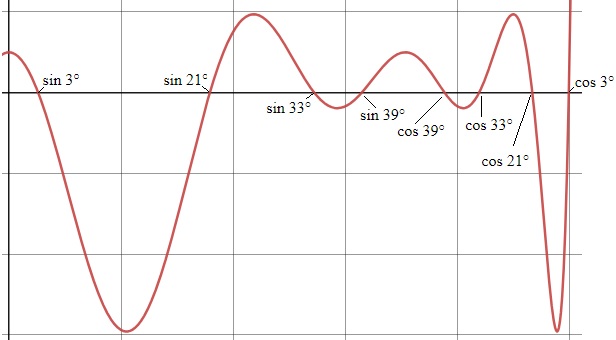
Here are a few more:
256x8 – 448x6 + 224x4 – 32x2 + 1 = 256(x2 – cos2 6°)(x2 – sin2 12°)(x2 – sin2 24°)(x2 – cos2 42°).
Its graph, for 0 < x < 1, is:

Here is another one:
16x4 – 8x3 – 16x2 + 8x + 1 = 16(x – cos 24°)(x – sin 42°)(x + sin 6°)(x + cos 12°).
Its graph, for – 1 < x < 1, is
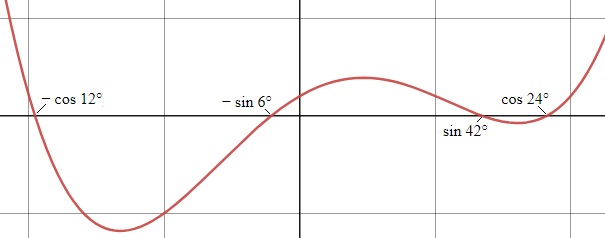
And yet another one:
256x8 – 512x6 + 304x4 – 48x2 + 1 = 256(x2 – sin2 9°)(x2 – cos2 9°)(x2 – sin2 27°)(x2 – cos2 27°).
Its graph, for 0 < x < 1, is

Angles that are not multiples of 3°
Consider the sine triple-angle identity,
sin 3t = – 4 sin3 t + 3 sin t.
Letting t = 10°, we have
sin 30° = – 4 sin3 10° + 3 sin 10°,
or
1/2 = – 4 sin3 10° + 3 sin 10°.
Multiplying by 2, we have
1 = – 8 sin3 10° + 6 sin 10°.
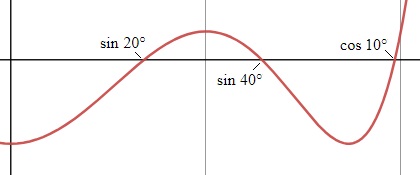
Thus, the polynomial 8x3 – 6x + 1 = 0 has sin 10° as a root, so that sin 10° is algebraic. Equivalently, the minimal polynomial for sin 10° is 8x3 – 6x + 1.
Using the cosine triple-angle identity and the angles t = 20° and t = 40°, we can show that cos 40° and –cos 20° are also roots of 8x3 – 6x + 1 and hence algebraic numbers. Thus,
8x3 – 6x + 1 = 8(x – sin 10°)(x + cos 20°)(x – cos 40°).
The graph is shown below:

Similarly, ±cos 10°, ±sin 40° and ±sin 20° are all roots of 64x6 – 96x4 + 36x2 – 3. That is,
64x6 – 96x4 + 36x2 – 3 = 64(x2 – sin2 40°)(x2 – sin2 20°)(x2 – cos2 10°).
The graph is shown below:
And one more: ±sin 5°, ±cos 5°, ±sin 25°, ±cos 25°, ±sin 35° and ±cos 35° are all roots of
4096x12 – 12288x10 + 13824x8 – 7168x6 + 1680x4 – 144x2 + 1.
This factors as:
4096(x2 – sin2 5°)(x2 – cos2 5°)(x2 – sin2 25°)(x2 – cos2 25°)(x2 – sin2 35°)(x2 – cos2 35°).
The graph is shown below:
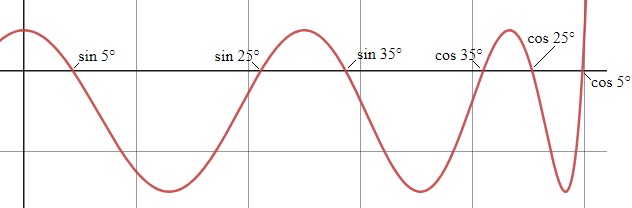
In this manner, we have taken care of all angles that are multiples of 5°, but not of 3°.
What about 1°?
The following construction results in a general way to illustrate the value of sin n°. Start with an isosceles triangle △ABC with two sides of length 1, and the remaining side of length x. Let the angle opposite x be (2n)°.
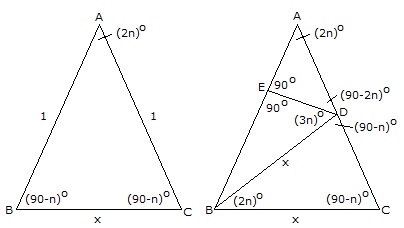
Continue the construction as follows: Draw segment BD such that its length is also x, then draw segment DE such that it meets segment AB at a right angle. Now label the lengths as follows: |DE| = x cos (3n) and |BE| = x sin (3n), so therefore, |AE| = 1 – x sin (3n). The Pythagorean formula gives the lengths of |AD| and |CD| as:
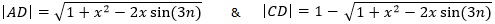
This is shown in the following figure
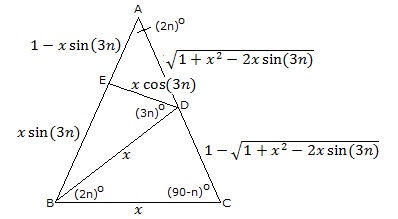
Now, drop a perpendicular from A to segment BC, and also a perpendicular from B to segment CD. In doing so, we have split the angle measurement (2n)° into n°. Importantly, note that triangles △ABC and △BCD are proportional. We can now define sin (n°) in two ways using the "opposite over hypotenuse" construction for right angles:
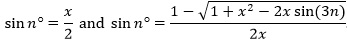
Relating the two expressions, we have:
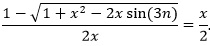
This simplifies to
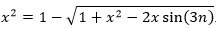
After squaring away the radical, the equation becomes
x4 – 3x2 + 2x sin (3n) = 0.
Since x = 0 produces a trivial case, we ignore it and divide out by x:
x3 – 3x + 2 sin (3n) = 0.
Let a be the positive root of this polynomial that is closest to 0. Therefore, sin (n°) = a/2, or a = 2 sin (n°). For example, to find sin 1°, let n = 1, which gives x3 – 3x + 2 sin (3°) = 0. A calculator shows that a = 0.0349048 is a root of this polynomial. Therefore, sin 1° = 0.0349048/2, or about 0.0174524, which is also confirmed by a calculator.
Since sin 10° and sin 9° are both algebraic (as are cos 10° and cos 9°, easily shown by the Pythagorean Identity), then
sin 1° = sin (10° – 9°) = sin 10° cos 9° – cos 10° sin 9°.
The product and sum/difference of two algebraic numbers is also algebraic. Thus, sin 1° is algebraic. Using the Pythagorean Identity, double-angle identities and so forth, all expressions of the form sin n° and cos n° are algebraic, where n is an integer.
By Scott Surgent. Please send feedback or error notification to me at surgent at asu dot edu.
This page originally published in 2012 and has gone through many iterations. Updated September 25, 2023.
| 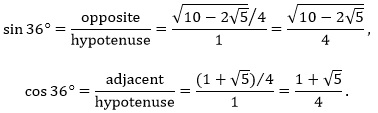
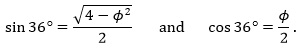








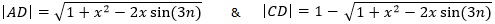
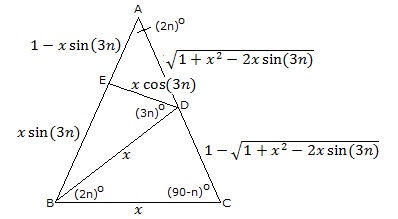
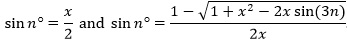
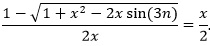
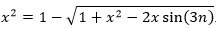
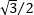 . Using the right-triangle trigonometry definitions sin x = opp/hyp and cos x = adj/hyp, we get sin 30° = 1/2 and cos 30° =
. Using the right-triangle trigonometry definitions sin x = opp/hyp and cos x = adj/hyp, we get sin 30° = 1/2 and cos 30° = 
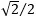 units each. This gives sin 45° = cos 45° =
units each. This gives sin 45° = cos 45° = 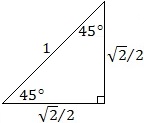

 . Splitting the 36-36-108 triangle in half forms a right triangle, a 36-54-90 triangle, with hypotenuse 1, long leg x/2 and short leg
. Splitting the 36-36-108 triangle in half forms a right triangle, a 36-54-90 triangle, with hypotenuse 1, long leg x/2 and short leg 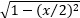 . Since x =
. Since x =