The Slowest Possible Baseball Pitch On August 7, 2021, Brock Holt, a position player pitching for the Texas Rangers, threw a pitch clocked at 31 miles per hour. It begs the question: what is the slowest possible pitch that could be thrown from a pitchers mound to the catcher? For this discussion, here are some reasonable assumptions about the pitch: The pitcher, starting on the pitching mound rubber (60 feet, 6 inches from home plate), will step forward one step, and release the ball overhand, slightly above his head. Taking into account the height of the pitcher's mound, and an average man's height of 6 feet, it is a reasonable assumption that the ball will be released 7 feet above the ground. Assume that the pitcher steps forward about 2.5 feet before releasing the ball. Since the pitcher's mound is 60 feet, 6 inches from home plate, assume that the ball is released 58 feet from home plate. Assume the pitch is a strike, so that it passes over home plate 3 feet off the ground. Assume no special spins or windups will be used. A slow pitch will be essentially a lob with a slight backspin that will have a negligible effect on the ball's trajectory. 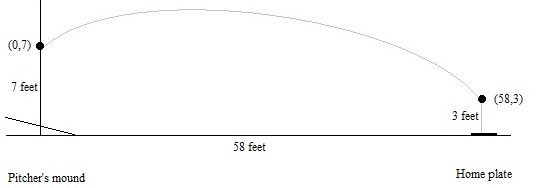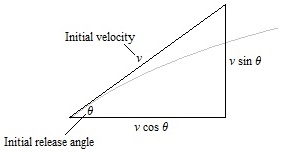The ball will follow a parabolic trajectory. Superimpose a coordinate axis system such that the point of release of the ball is 0 feet horizontally, 7 feet vertically (hence, the ordered pair (0,7)), and that the ball passes over home plate, 58 feet away, at 3 feet above the ground. This gives another ordered pair (58,3). The ball will be released at an initial speed denoted by v, and at an initial angle θ. The parameter t will be used to represent time, in seconds. The distance unit will be feet, and the ball's speed will be in feet per second, which we can convert to miles per hour at the end. Start with a vector-function representation for acceleration due to gravity. All objects on Earth must obey this rule: a(t) = 0i −32j. The 0 represents the no effect of gravity in the horizontal direction, and the −32 represents the gravitational constant for acceleration, which is 32 feet per second2, the leading negative indicating that gravity attracts the ball downward. Gravity only affects objects vertically. Integrating, we get a velocity vector-function: v(t) = vxi + (−32t + vy)j, where constants vx and vy represent the initial velocities of the ball in the x-direction and y-direction respectively. We decompose a right triangle, so that vx = v cos θ and vy = v sin θ. We don't yet know v, and the angle can vary too. For now, we will leave these expressions in their generalized form. Thus, the velocity function is: v(t) = (v cos θ)i + (−32t + v sin θ)j. The magnitude v is decomposed into its horizontal and vertical components. Integrating one more time, we derive a displacement vector-function for the ball: d(t) = ((v cos θ)t + dx)i + (−16t2 + (v sin θ)t + dy)j, The values dx and dy are the initial positions of the ball in the x and y directions, respectively. It is always possible to superimpose a coordinate system so that the initial x-position is 0. Thus, the initial y position is 7 and we get dx = 0 and dy = 7: d(t) = ((v cos θ)t)i + (−16t2 + (v sin θ)t + 7)j. There are three variables (one free variable t and two parameter variables v and θ) defining the ball's trajectory. Here's where the other ordered pair, (58,3), comes into play. The two components of the displacement function is set to these values: (v cos θ)t = 58   &   −16t2 + (v sin θ)t + 7 = 3. In the first equation, solve for v: v = 58/(t cos θ). This is substituted for v in the second equation (note: the constants are combined to the right side, which explains the −4). Observe that in the second term, variable t cancel one another, and the resulting trigonometric expression sin θ/cos θ = tan θ: −16t2 + 58 tan θ = −4. This leaves an equation where t appears just once as a squared quantity. Thus, it is easy to isolate t: t = sqrt((4 + 58 tan θ)/16). If we know the release angle θ of the ball, this formula then gives the time, in seconds, required for the ball to reach home plate. Now knowing t, we use the formula given above a few lines to find v. As an example, suppose the ball is released at an angle of 30°. Then the time t is t = sqrt((4 + 58 tan (30°)/16) ≈ 1.53065 seconds. and the velocity v is therefore v = 58/(1.53065 cos (30°)) ≈ 43.7544 feet per second. This is in feet per second. To convert into miles per hours, use the conversions that 1 mile = 5,280 feet, and that 1 hour = 3,600 seconds. This is equivalent to multiplying by the ratio 3,600/5,280, which simplifies into the fraction 15/22. Thus, the speed of the pitch, in miles per hour, is (43.7544 ft/sec)(15/22) ≈ 29.83 miles per hour. This is slower than Holt's 31 miles-per-hour toss. Can it be slower? The velocity expression can be stated as a function of θ by making the substitution: v = 58/((sqrt(4 + 58 tan θ)/16) cos θ). This is simplified: v(θ) = 116 sec θ/sqrt(1 + 14.5 tan θ). A few values for θ are chosen and the resulting velocities found: v(0°) = 116 sec (0°)/sqrt(1 + 14.5 tan (0°)) ≈ 116 feet per second ≈ 79.09 miles per hour. v(45°) = 116 sec (45°)/sqrt(1 + 14.5 tan (45°)) ≈ 41.668 feet per second ≈ 28.41 miles per hour. v(55°) = 116 sec (55°)/sqrt(1 + 14.5 tan (55°)) ≈ 43.407 feet per second ≈ 29.595 miles per hour. It appears that releasing the ball at a 45° angle will result in a pitch moving at 28.41 miles per hour. Is this the slowest possible pitch? Graphing v as a function of θ gives the following graph: We find the θ-value needed to release the ball so that the velocity value is minimized. Using a graphing utility, this point is at approximately (43.027, 41.622), meaning that the ball should be released at an angle of 43.027°, which means the ball will move at about 41.622 feet per second, or 28.38 miles per hour. Keep in mind that the initial assumptions from the beginning were chosen as reasonable, but still arbitrarily. For example, repeating this process with a release height of 6 feet, and a stride of 4 feet, and the ball moving over home plate at 4 feet off the ground, will result in slightly different functions. However, the values that result will all be in the ball-park (pun intended) of a slowest pitch being about 25-28 miles per hour. It would appear that this range gives the absolute slowest possible pitch that could be thrown for a strike.   Prepared by Scott Surgent. Report errors or questions to scott dot surgent at gmail dot com. (October 2021)