|
(PDF)
Given a point P0 = (x0,y0,z0) and a vector n = 〈a, b, c〉, a plane that passes through P0 and is normal (orthogonal) to n has the equation which simplifies to ax + by + cz = d, where d = ax0 + by0 + cz0.
Example 13.1: Find the equation of the plane passing through P0 = (−3,9,1) and normal to n = 〈7,3,−5〉. Solution: The plane has the equation Simplifying, we have 7x + 21 + 3y − 27 − 5z + 5 = 0 7x + 3y − 5z = 1.
Example 13.2: State a vector that is normal to the plane 2x − 4y + 3z = 12. Solution: There are infinitely-many possible vectors. One is 〈2,−4,3〉, which is found by reading the coefficients of x, y and z. Any non-zero multiple of 〈2,−4,3〉 is also a vector normal to the plane. Example 13.3: Let −2x + 7y + 4z = −7 be a plane in R3. Find the equation of the line normal to the plane that passes through the point (1,−3,5) on the plane. Solution: The line is parallel to (in the direction of) n = 〈−2,7,4〉, so the line is given by Example 13.4: Find the point of intersection of the line 〈x,y,z〉 = 〈4 − t, 2 + 3t, 3 − 5t〉 and the plane 6x + 2y − 3z = 79. Solution: Substitute the equations for x, y and z into the plane, and solve for t: 24 − 6t + 4 + 6t − 9 + 15t = 79 15t = 60 t = 4. Now substitute t = 4 into the equations for the line: This is a vector, but if referenced from the origin, its head lies at the point (0,14,−17). Example 13.5: Find the equation of the plane passing through the points A = (1,3,4), B = (−3,2,6) and C = (1,0,−6). Solution: From the three points, form two vectors. For example, vectors AB and AC: Next, find a vector n normal to AB and AC by finding the cross product AB × AC: Any non-zero multiple of n will suffice, so we divide through by 4, getting n = 〈4,−10,3〉. Using any one of the three given points, we now find the equation of the plane. We'll use A first, then check our work with B and C. Using A = (1,3,4) and n = 〈4,−10,3〉, we have 4x − 4 − 10y + 30 + 3z − 12 = 0 4x − 10y + 3z = −14. Verify this is correct by substituting the coordinates for points B and C into the equation: C = (1,0,−6): 4(1) − 10(0) + 3(−6) = 4 − 18 = −14, true. Example 13.6: Show that the equation of a plane passing through the axis-intercepts (a,0,0), (0,b,0) and (0,0,c) is x/a + y/b + z/c = 1. Solution: Form two vectors: The vector from (0,b,0) to (0,0,c) is v = 〈0 − 0, 0 − b, c − 0〉 = 〈0,−b,c〉. Their cross product is u × v = 〈bc,ac,ab〉, and using (a,0,0) as a point in the plane, the plane's equation is bcx − abc + acy + abz = 0 bcx + acy + abz = abc. Now, divide through by abc: This is a handy formula for finding the equation of a plane given its axis-intercepts. Example 13.7: Find the acute angle formed by the intersection of the planes x + 3y − 2z = 5 and 4x − y + 5z = −2. Solution: The respective normal vectors of each plane are n1 = 〈1,3,−2〉 and n2 = 〈4,−1,5〉. The angle between these two planes is the same as the angle between the two normal vectors: However, planes always intersect at an acute angle (except in the case where they are orthogonal). The preferred answer is the supplement: 180° − 111.79° = 68.21°. Example 13.8: Find the acute angle formed by vector v = 〈1,4,3〉 and plane 2x + y + 5z = 4. Solution: The plane's normal vector is n = 〈2,1,5〉, so the angle between v and n is Visually, v and n are on the same side of the plane, as their angle is acute. Note that 41.24° is the angle between v and n, so the angle between v and the plane is the complement, 90° − 41.24° = 48.76°. 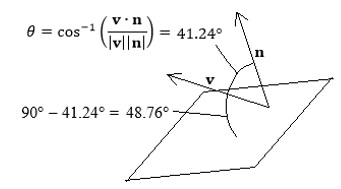
Find the angle between v and n first, then find the complement. Example 13.9: Find the acute angle formed by vector v = 〈2,1,−8〉 and plane x + 2y + z = 4. Solution: The plane's normal vector is n = 〈1,2,1〉, so the angle between v and n is In this example, the vector n is on one side of the plane, and v on the opposite side. Since the angle from n to the plane is 90°, the remainder, 101.34° − 90° = 11.34°, is the desired angle. 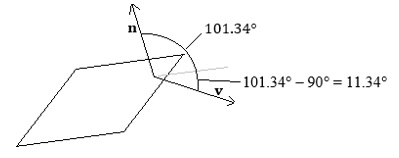
Vectors v and n lie on opposite sides of the plane, so the acute angle v makes with the plane is found by subtracting 90 degrees. Another way to view this is to use n = 〈−1,−2,−1〉, which would have given us Thus, v and n are on the same side of the plane, and the complement gives us 90° − 78.66° = 11.34°, the desired angle. Example 13.10: Find the parametric equation of the line formed by the intersection of the planes x − 3y + 2z = −16 and 2x + y − 7z = 18. Solution: The planes are not parallel since their normal vectors, n1 = 〈1,−3,2〉 and n2 = 〈2,1,−7〉, are not scalar multiples of one another. Had the planes been parallel, they would not intersect (unless they were the same coincident plane). To find the parametric equation of the line, we need a point on this line of intersection, and a direction vector parallel to the line of intersection. For a point on the line of intersection, set one variable to 0, and solve for the other two variables. Let x = 0 in both equations. This results in a system y − 7z = 18. The solution is y = 4 and z = −2. Thus, (0,4,−2) is a point on the line of intersection of the two planes. For the direction vector, we note that it will be orthogonal to both normal vectors of each plane. Thus, we can find a vector parallel to the line of intersection by finding the cross product of the two normal vectors. We get n1 × n2 = 〈19,11,7〉. Therefore, the line of intersection of the two planes is given parametrically by Example 13.11: Find the equation of the plane passing through P0 = (7,3,−11) and parallel to the plane 2x − y + 6z = 1. Solution: The two planes are parallel, so they share the same normal vector n = 〈2,−1,6〉. Thus, the plane's equation is 2x − 14 − y + 3 + 6z + 66 = 0 2x − y + 6z = −55.
Parametric Representation of a Plane A plane can also be represented parametrically in vector form. Assume that a plane passes through P0 = (x0,y0,z0) and that v1 and v2 are two (non-parallel) vectors that lie within the plane. The plane can then be written as where s and t are independent parameter variables that may assume any real-number value, and that v0 is the vector whose head points to P0 when s = 0 and t = 0. Example 13.12: Write the plane 3x + 2y + z = 5 in parametric form. Solution: Any of the three variables can be isolated, leaving one dependent variable and two independent variables. In this case, we isolate z: Now, let x = s and y = t. We now have y = t z = 5 − 3s − 2t. Observe what happens when we "zero-fill" the missing terms: y = 0 + 0s + 1t z = 5 − 3s − 2t. The vectors v0, v1 and v2 can be inferred from the columns in the previous step: 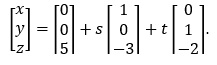
Thus, the plane 3x + 2y + z = 5 written in parametric form is
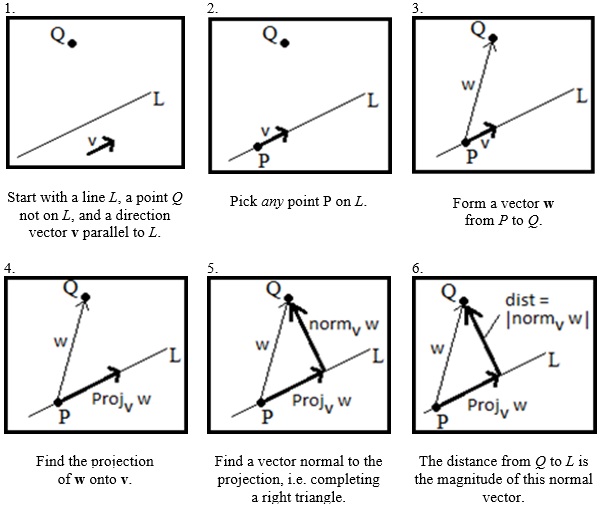
Example 13.13: Rewrite the plane given by 〈x,y,z〉 = 〈0,0,2〉 + s〈1,0,4〉 + t〈0,1,−7〉 into the form ax + by + cz = d. Solution: Reading across component by component, we have y = 0 + 0s + 1t z = 2 + 4s − 7t. In this case, we have x = s and y = t, so the last equation can be written as Thus, the plane 〈x,y,z〉 = 〈0,0,2〉 + s〈1,0,4〉 + t〈0,1,−7〉 can be written as −4x + 7y + z = 2. Example 13.14: Rewrite the plane given by 〈x,y,z〉 = 〈1,3,4〉 + s〈2,−1,5〉 + t〈−3,8,1〉 into the form ax + by + cz = d. Solution: Reading across component by component, we have y = 3 − s + 8t (2) z = 4 + 5s + t. (3) We need to write s and t in terms of x and y. From the first two equations (1) and (2), we have −s + 8t = y−3. We eliminate s by multiplying the bottom row by 2, then adding: −2s + 16t = 2y − 6, which gives 13t = x + 2y − 7. Thus, t = (1/13)(x + 2y − 7). In a similar way, we can eliminate t, in which case we have s = (1/13)(8x + 3y − 17). These are substituted into equation (3): This simplifies to Multiplying by 13 to clear fractions, we have 13z = 41x + 17y − 40. Thus, the plane can be written as 41x + 17y − 13z = 40. Example 13.15: Find the equation of the plane passing through P0 = (−3,9,1) and normal to n = 〈7,3,−5〉. (This is a repeat of Example 13.1) Solution: We need two vectors, v1 and v2, in the plane. These two vectors will be orthogonal to n. For example, if we choose the x-component of v1 to be 0, then v1 = 〈0,5,3〉 is orthogonal to n and hence, in the plane. In a similar way, we could let the y-component of v2 be 0, and so v2 = 〈5,0,7〉 is orthogonal to n and also in the plane. Noting that v0 corresponds to point P0 = (−3,9,1), we have Is this the same as 7x + 3y − 5z = 1, the result from Example 13.1? Let's find out. Reading component-wise, we have y = 9 + 5s + 0t z = 1 + 3s + 7t. Solving for t in the first equation gives t = (1/5)(x + 3), and doing similar in the second equation gives s = (1/5)(y − 9). These are substituted into the third equation: Clearing parentheses, we have Multiplying by 5, we have 5z = 7x + 3y − 1. Rearranging terms, we have 7x + 3y − 5z = 1. 14. Distances in R3 We use projections to find the shortest distances between a point and a line, between two non-intersecting lines, between a point and a plane, and between two parallel planes. The shortest distance is defined to be a line that meets the objects orthogonally. Example 14.1: Find the shortest distance between the line 〈x,y,z〉 = 〈1, 2, −1〉 + t〈2, −3, 4〉 and the point Q = (4,8,3). Solution: Choose any point P on the line. For example, when t = 0, we have P = (1, 2, −1). Then find the vector from P to Q, which is w = 〈4 − 1, 8 − 2, 3 − (−1)〉 = 〈3, 6, 4〉. Meanwhile, the directional vector of the line is v = 〈2, −3, 4〉. The projection of w onto v is: The normal vector is found by subtracting projv w from w: The magnitude of this normal vector is the distance from the point Q to the line:
Example 14.2: Find the shortest distance between point Q = (1,4,3) and plane x − 3y + 2z = 6. Solution: Pick any point P in the plane by choosing values for two of the variables and solving for the third. If x = 0 and y = 0, we get z = 3, so a point in the plane is P = (0,0,3). The vector v from P to Q is v = 〈1,4,0〉. The normal vector to the plane is n = 〈1,−3,2〉. Project v onto n: The magnitude of this vector is the distance from Q = (1,4,3) to the plane x − 3y + 2z = 6: • • • • • • • • • • •
• • • • • • • • • • • When a vector w is projected onto a vector v, this produces a vector called projv w. This can be viewed as one leg of a right triangle, with w being the hypotenuse. The other leg is called normv w In vector addition, we have: Their magnitudes are related by the Pythagorean Theorem:
• • • • • • • • • • • Example 14.3: Find the shortest distance between the parallel planes x − 3y + 2z = 6 and −2x + 6y − 4z = 1. Solution: The vector n = 〈1, −3, 2〉 is orthogonal to both planes. Choose any point on each plane. From the plane x − 3y + 2z = 6, we use the point A = (0,0,3), and from the plane −2x + 6y − 4z = 1, we use B = (−1/2, 0, 0). The vector v from A to B is v = 〈 1/2, 0, 3〉. We then project v onto n: The magnitude of this vector is the shortest distance between the two planes:
Example 14.4: Find the shortest distance between the lines L1: 〈x, y, z〉 = 〈1, −2, 6〉 + t〈1, −5, 4〉 and L2: 〈x, y, z〉 = 〈0,8,1〉 + s〈4, −7, 3〉 Solution: These lines are skew. Thus, they will not intersect. Two skew lines in R3 can always be placed within two parallel planes, so that this example is nearly identical to the previous example. From the first line, we have a point A = (1, −2, 6) and from the second line, we have a point B = (0,8,1), and the vector v from A to B is v = 〈−1, 10, −5〉. The normal vector n to the two planes that each contain one of the lines is found by finding the cross product of the two direction vectors of each line. From the first line, we have v1 = 〈1, −5, 4〉 and from the second line, we have v2 = 〈4, −7, 3〉. Their cross product is However, we can use any non-zero multiple of n for this example, so n = 〈1,1,1〉 will suffice, since the projection step will extend n to the desired length. Now project v onto n: The distance is the magnitude of this projection vector:
|