|
Solving a Cubic Polynomial
Below is a general cubic polynimal set to zero:
Ax3 + Bx2 + Cx + D = 0,
where A, B, C and D are integers, and A ≠ 0. Dividing through by A, we get an equivalent cubic polynomial equation of the form
x3 + bx2 + cx + d = 0,
where b, c and d are rationals (possibly integers), and the leading coefficient is 1.
The Depressed Cubic
A depressed cubic lacks the quadratic (squared) term, for example:
x3 + mx + n = 0.
Any cubic polynomial of the form x3 + bx2 + cx + d = 0 can be depressed by applying a shift to the variable, letting x = w + h, where h will be determined. Make the variable switch:
(w + h)3 + b(w + h)2 + c(w + h) + d = 0.
Expand the parentheses:
(w3 + 3w2h + 3wh2 + h3) + b(w2 + 2wh + h2) + c(w + h) + d = 0.
Clear parentheses by distribution:
w3 + 3w2h + 3wh2 + h3 + bw2 + 2bwh + bh2 + cw + ch + d = 0.
Now, collect terms according to powers of w:
w3 + w2(3h + b) + w(3h2 + 2bh + c) + (h3 + bh2 + ch + d) = 0.
We don't want the w2 term, so to make it disappear, set 3h + b = 0, which forces h = −b/3. We make this substitution for all h in the above equation:
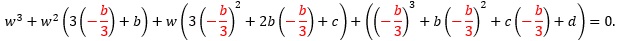
Note that (−b/3)3 = −b3/27 and that (−b/3)2 = b2/9:
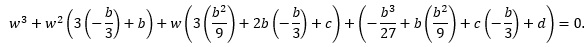
The expression 3(−b/3) + b = 0, as desired. It simply vanishes. The remaining terms are simplified:
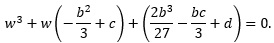 ➀ ➀
Example: Given x3 + 12x2 − 4x + 6 = 0, find its corresponding depressed cubic expression.
Solution: Note that b = 12, c = −4 and d = 6. Make these substitutions in the above formula marked ➀:
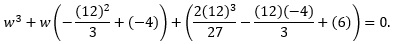
Simplify the constants:
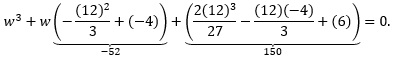
Thus, the corresponding depressed cubic polynomial of x3 + 12x2 − 4x + 6 = 0 is w3 − 52w + 150 = 0. They differ by a horizontal shift, in this case the depressed cubic is shifted 4 units to the right of the original cubic. ▮

The graph of x3 + 12x2 − 4x + 6 (in red), and the graph of its corresponding depressed cubic w3 − 52w + 150 (in blue).
Note that the shift is h = −12/3 = −4, so that the variable switch is w = x − 4, indicating a shift right of 4 units.
(Graph: Desmos.com --- Click to enlarge)
Solving The Depressed Cubic
Consider the depressed cubic equation of the form below:
w3 + mw + n = 0.
We make one more variable substitution, w = u + k/u, where u is a variable and k is a constant to be determined momentarily:
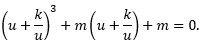
Expanding the expression (u + k/u)3 gives u3 + 3u2(k/u) + 3u(k/u)2 + (k/u)3. This is substituted, and the equation simplified:
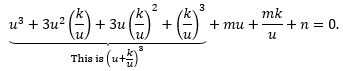
One more simplification step:
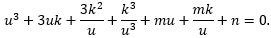
The terms are re-ordered by powers of u:
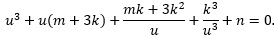
Now is the time to choose a value for k. Note that we can force the expression m + 3k = 0 by choosing k = −m/3. This also forces the expression mk + 3k2 = 0, too, so that both of these terms vanish. We are left with:
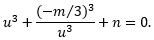
Multiply through by u3 and re-order the terms by descending powers of u:
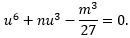
This is a quadratic-in-form equation, by treating u6 = (u3)2. Thus, it can be solved by using the quadratic formula:
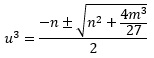
Taking a cube-root, we can find u:

Thus, working backwards and recalling that w = u + k/u, we have:
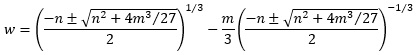
And lastly, recall that from the original non-depressed cubic, x3 + bx2 + cx + d, that x = w + h, where h = −b/3. Thus, by working backwards through the variable changes, we can find an expression for x that solves the given cubic polynomial.
Let's do a couple examples.
Example: Solve x3 + 2x − 3 = 0. In this case, we can see that x = 1 is a solution. Let's see how well the process works.
Solution: Since this cubic is already depressed, we see that m = 2 and n = −3. Thus,
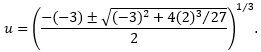
Simplified:
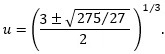
Thus, since x = u − (2/3)/u, we have:
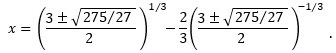
Assuming the principal square root, i.e. the positive root, we have
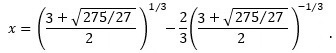
Believe it or not, this is the number 1. The process worked! ▮

Wolframalpha confirms that the expression x = [(3 + sqrt(275/27))/2]1/3 − (2/3)[(3 + sqrt(275/27))/2]−1/3 does in fact equal 1.
(Click to enlarge)
Let's continue with this problem. Now that we know that x = 1 is a root, we can divide the polynomial x3 + 2x − 3 by x − 1. The polynomial factors as
x3 + 2x − 3 = (x − 1)(x2 + x + 3).
Using the quadratic formula on the quadratic factor, we can find the other two solutions:
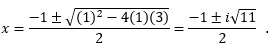
Notice what happens when we use the negative square root from the solution process:
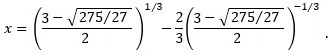
This is equivalent to x = (−1 + i sqrt(11))/2, as shown below by Wolframalpha. This is one of the roots found by the quadratic formula moments ago.

Wolframalpha confirms that the expression x = [(3 − sqrt(275/27))/2]1/3 − (2/3)[(3 − sqrt(275/27))/2]−1/3 equals (−1 + i sqrt(11))/2.
(Click to enlarge)
Prepared by Scott Surgent. Report errors or questions to surgent@asu.edu. (June 2021)
|