Bobby Bonilla's Contract Explained

In 2000, baseball player Bobby Bonilla was released by the New York Mets, who owed him $5.9 million. The Mets agreed to pay it out in 25 installments between 2011 and 2035 inclusive. Before then, the original $5.9 million would grow at 8% compounded annually for 11 years (2000-2010 inclusive).

The table below was found online (www.goldin.co), an addendum to his contract that shows exactly how the money accrues interest then is amortized to 0.

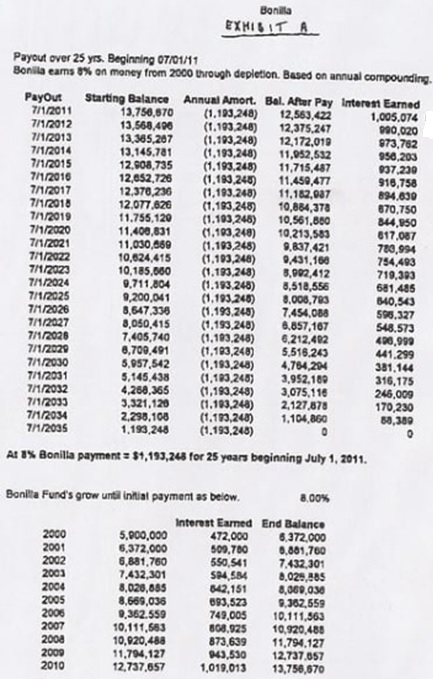
The bottom half of the sheet shows the accrual period. The principal P is the $5.9 million, the annual percentage rate r is 8%, written 0.08, and the period t is in years. Note that 2000-2010 inclusive is 11 years. The formula for the future value of compounded interest on a principal is

PV = P(1 + r)t.

Using the formula, substitute in the values for P, r and t:

PV = P(1 + r)t = 5,900,000(1.08)11 = $13,756,670.

This is the figure shown on the bottom right of the sheet. This is called the "Present Value" (abbreviated PV) because as of 2011, when the payments to Bonilla begin, it will be considered the present value of the fund used to pay him.

Let's assume for the moment we don't know how much Bonilla is to be paid every year starting in 2011. Call this lower-case p.

The Present Value, $13,756,670, will be amortized over a period of 25 years until the value of the fund is $0. It's important to state that the Present Value is not static. It will not be divided into 25 equal chunks to be paid to Bonilla. In amortization, the Present Value continues to grow, while at regular intervals, a payment (p) is subtracted. So it is a consistent "growth-subtraction" routine that plays out over a 25-year term, where the last "subtraction" brings the fund to 0.

In the first year (2011, denoted n = 1 so that we can track the number of years easier), the first payment p is subtracted from the present value PV. This is the expression PV − p. This is the new value of the Bonilla fund heading into 2012.

In the second year (2012, or n = 2), two things happen to the fund's value in the following order: (1) it accrues interest by 8%, and (2) then payment p is subtracted. This is the new value of the Bonilla fund heading into 2013. This is written as the expression

1.08(PV − p) − p.

This can be described in more detail. To "increase by 8%" means to multiply the fund's value (PV − p) by 1.08, so we have 1.08(PV − p); then from that, payment p is subtracted. That's how we get 1.08(PV − p) − p. This can be simplified by multiplying to clear parentheses:

1.08PV − 1.08p − p.

In the third year (2013, n = 3), the same two things happen: (1) the fund's value from 2012 accrues 8% interest, and (2) payment p is subtracted. The value of the Bonilla fund heading into 2014 is

1.08(1.08PV − 1.08p − p) − p.

Multiplying to clear parentheses, this is

1.082PV − 1.082p − 1.08p − p.

In the fourth year (2014, n = 4), we continue the same scheme. Note that the expression from the previous year gets "fitted" into the parentheses in the expression for the current year. Thus, the value of the Bonilla fund heading into 2015 is

1.08(1.082PV − 1.082p − 1.08p − p) − p.

Multiplying to clear parentheses, this is

1.083PV − 1.083p − 1.082p − 1.08p − p.

Let's collect this into a table and note a pattern:

Year
n
Value of the Bonilla fund after payment
2011
1
PV − p
2012
2
1.08PV − 1.08p − p
2013
3
1.082PV − 1.082p − 1.08p − p
2014
4
1.083PV − 1.083p − 1.082p − 1.08p − p

The pattern suggests a way to describe the value of the Bonilla fund without having to go through the intermediate steps. For example, in 2015 (n = 5), going by the pattern, the value of the fund will be

1.084PV − 1.084p − 1.083p − 1.082p − 1.08p − p.

Observe that the highest exponents of the terms is always one less than the n-value representing the given year. Thus, in 2035 (n = 25), the value of the Bonilla fund would be written

1.0824PV − 1.0824p − 1.0823p − 1.0822p − . . . − 1.083p − 1.082p − 1.08p − p.

Factor −p from the rightmost terms. This gives:

1.0824PV − p(1.0824 + 1.0823 + 1.0822 + . . . + 1.083 + 1.082 + 1.08 + 1).

The terms within the parentheses are a geometric series, reading right to left, the first term is a = 1 and the common ratio is r = 1.08. The formula for the sum of the first n terms of a geometric series is

S = a(rn − 1) ÷ (r − 1).

Note that the series 1.0824 + 1.0823 + 1.0822 + . . . + 1.083 + 1.082 + 1.08 + 1 has 25 terms. Thus, the terms within the parentheses can be summarized as a geometric sum:

S = 1(1.0825 − 1) ÷ (1.08 − 1),    which simplifes to    S = (1.0825 − 1) ÷ 0.08.

Finally, the long expression representing the value of the Bonilla fund in 2035 is

1.0824PV − p((1.0825 − 1) ÷ 0.08)

The plan was that the value of the Bonilla fund after the last payment would be $0, and the fund fully amortized. This expression above is set to 0 and solved for p:

1.0824PV − p((1.0825 − 1) ÷ 0.08) = 0,    so that    p = 1.0824PV ÷ ((1.0825 − 1) ÷ 0.08)

Substituting PV = $13,756,670 and using a calculator, we get p = $1,193,248.19.

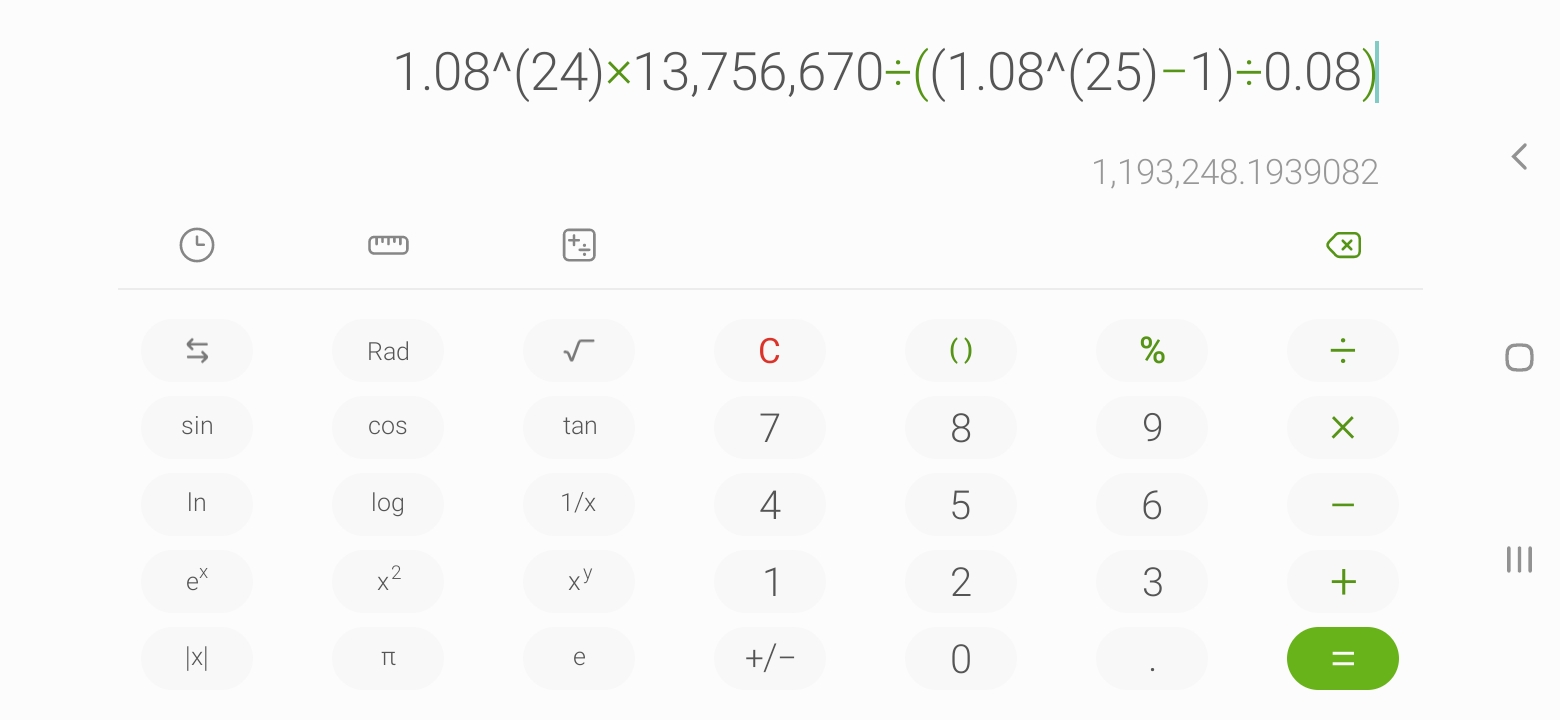
And this is what Mr. Bonilla receives every year between 2011 and 2035.

 

PDF Version

 

 

 

By Scott Surgent. Please send feedback to me at scott dot surgent at gmail. Updated 11/9/22.