|
Preliminary: Definition of Terms For purposes of this discussion, I want to first set straight the difference between the words "elevation" and "altitude". These two words are often used interchangeably, but they are not synonyms. They imply different meanings and should not be used interchangeably. Elevation is the height of a point on land relative to mean sea level, which is deined to be Elevation 0 feet (or m). Elevations always occur on land. Altitude is the height of an object in air, relative to the ground below it. Altitudes always occur in air. A mountain climber standing on Mount Everest will be at an elevation of 29,035 feet (or whatever it is these days), and at an altitude of 0 feet, assuming he is not jumping in the air at that very moment. A person is standing on ground that has elevation 1,500 feet throws a ball into the air. The ball rises 50 feet above the ground. The ball's altitude is 50 feet, since it is measured relative to the ground below it, not mean sea level. When the ball hits the ground and stops bouncing, its elevation is then 1,500 feet. The exception to this nomenclature is discussing a flying airplane. Since the airplane is not on the ground, it will have an altitude figure, but since the ground's elevation below it will vary as the airplane moves over it, it is easier to simply refer to the airplane's altitude relative to mean sea level, rather than have to continually calculate its altitude over the point on the ground underneath the airplane. For large jetlines that reach a cruising altitude of 32,000 feet (for example), no distinction in altitude is made when flying over the Rocky Mountains versus flying over low-lying Central Plains. However, for smaller airplanes and helicopters, its altitude is often figured relative to the ground below it since these objects generally stay closer to the ground, where knowing one's clearance (altitude) is much more important than when up high in a jetliner. Prominence: Two Models The prominence of a mountain is the difference in elevation between the summit and the lowest point along the ridge that connects the mountain to a higher mountain. However, a single mountain usually connects to more than one higher mountain via more than one ridge. The lowest points of the set of ridges that connects a mountain to other higher mountains are identified, and the highest value of these low points is identified. This is called the mountain's defining saddle or key col. Thus, to be more accurate, the mountain's prominence is the difference between the mountain's elevation and its key col. This makes sense with pictures. The Receding Waters & Islands Model Consider a flood that covers all but the tops of mountains. The mountain tops would then be islands. Now, suppose the waters recede. At some point, the individual islands will start to connect to one another, forming larger islands. For a particular mountain, the moment it connects to a larger island such that this new island has points of elevation higher than the given mountain, this point of connection becomes its defining saddle, or key col. The prominence of the mountain is then the vertical differential between this key col, and the summit.
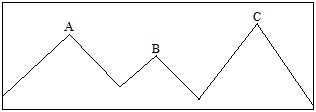
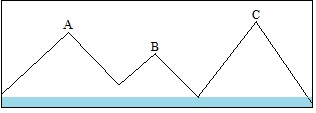
In the above figure, A, B and C represent mountains. B connects to A and C via two low points on a ridge. The two low points are identified, and the higher of the two is then defined as B's key col. Notice that the low point between B and A is higher than the low point between B and C. Thus, the prominence of B would be measured from the low point between B and A. Here's a "flooded" view of this same situation:
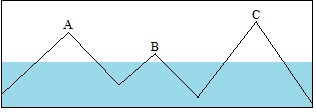
Mountains A, B and C are three separate islands. Their passes are covered by water. Now, the waters recede:
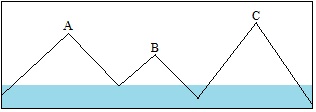
The pass between B and A appears first. B and A are now connected as a larger island, still separated from C. Since A is higher than B, B's key col is now found, it being the pass connecting B to A. B's prominence can now be determined.
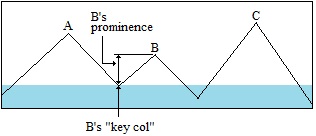
What about A's prominence? To find the prominence of A, we need to find its own key col connecting A to higher land. In terms of finding A's prominence, all lower mountains, including B, play no role. Suppose the waters recede more:
Now the island containing A is connected to a larger island with higher land, that being mountain C. Mountain A's key col in the image above is the saddle between B and C. Note that B plays no role in this calculation. It's as if B is not there.
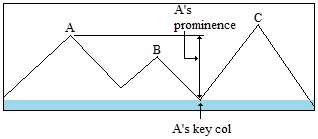
Mountain C's prominence would be found in the same way, expanding ever outward to encompass more land. In this manner, a lineage is developed. In the above image, B's parent is A, and A's parent is C, and so on. All lineages lead to the highest point on the land mass. Such "land mass" highpoints have prominence figures calculated from sea level. Prominence Using Topographical Maps and Contour Lines Another way to describe prominence is as follows: It is the difference between a mountain's summit elevation and the lowest contour surrounding the peak, but no higher peak. Consider the example below, showing Darton Dome in northern Arizona.
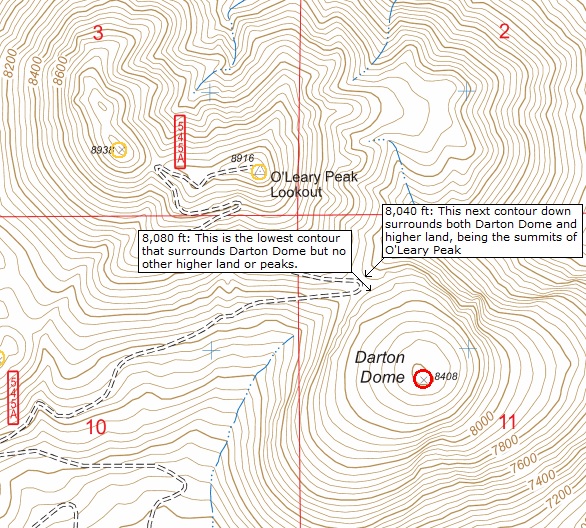
Darton Dome has a summit elevation of 8,408 feet. Look carefully at the contours that surround it. They are spaced every 40 feet. The contour representing 8,080 feet surrounds Darton Dome and no higher land. The next contour down, representing 8,040 feet, surrounds Darton Dome and higher land, the summits of O'Leary Peak. The pass connecting Darton Dome to the higher land is between 8,040 feet and 8,080 feet, or interpolated as 8,060 feet. Thus, Darton Dome's prominence is approximately 8,408 − 8,060 = 348 feet. Most topographical maps list a summit's elevation, but not elevations for passes. Thus, a pass's elevation must be interpolated from the contour lines surrounding it. This results in three flavors of prominence: • Clean. The minimum possible prominence based on a reading of the contours. This is the absolute lowest figure of a mountain's potential prominence. In the above image, the lowest contour that surrounds Darton Dome and no higher land is at 8,080 feet. Thus, Darton Dome's clean prominence is 8,408 − 8,080 = 328 feet. • Optimistic. This is the maximum possible prominence. It is nearly guaranteed that the mountain's prominence will not exceed this figure. In the above image, the next lower contour that surrounds Darton Dome and higher land is at 8,040 feet. Thus, Darton Dome's optimistic prominence is 8,408 − 8,040 = 368 feet. In such cases, it is common to average the two figures, so that Darton Dome's prominence is about 348 feet. • True. In the rare case when a pass's elevation is known, then the difference in elevation between the summit and pass can be calculated "exactly", insofar as the accuracy of these figures is stated and trusted. Things can get a little messy when a summit elevation is not given. In such a case, its elevation must be inferred from the highest contour, so this adds an extra layer of uncertainty to the prominence calculation. The definitive book on this subject is The Finest peaks: Prominence and Other Mountain Measures, by the late Adam Helman and available at Amazon. Prominence figures are given for most major mountains in the world and discussions as to how they were found.
|